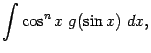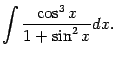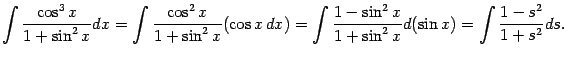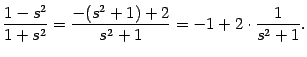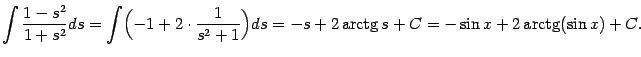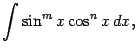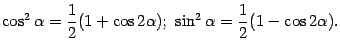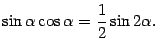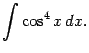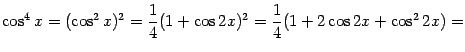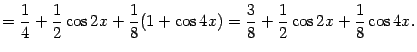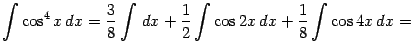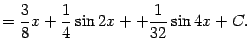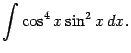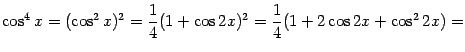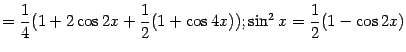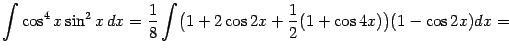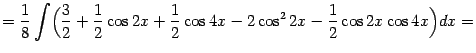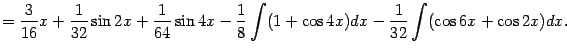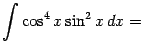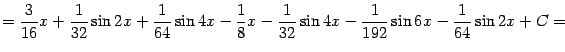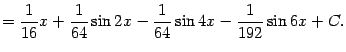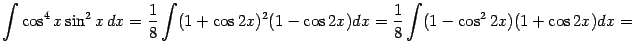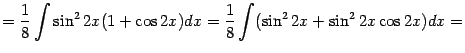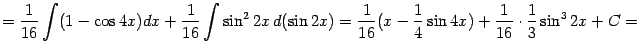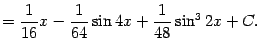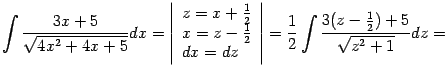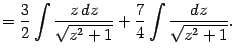‹-- Назад
1. Интегралы, содержащие квадратный трёхчлен. Рассмотрим интегралы, подынтегральная функция в которых содержит квадратный трёхчлен 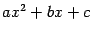 , где
, где 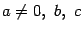 -- некоторые постоянные, вида
-- некоторые постоянные, вида
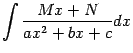
и
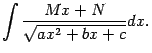
(Заметим, что в числителе дроби должно стоять линейное выражение
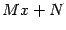
, где
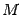
и
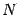
-- постоянные; при этом какой-либо из постоянных не запрещается быть равной 0.)
Такие интегралы приводятся к табличным следующим способом. Нужно выделить из квадратного трёхчлена выражение, равное полному квадрату, сделав такое преобразование:
После этого сделаем линейную замену
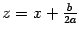
и получим интеграл одного из видов:
при некоторых постоянных
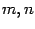
и
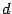
. Далее разбиваем интеграл на два слагаемых и в первом, в числителе подынтегральной функции содержащем
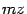
, делаем замену
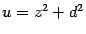
,
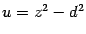
или
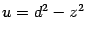
, согласно тому, что стоит в знаменателе. После этого первое слагаемое приводится к табличному интегралу. Второе слагаемое, с
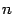
в числителе подынтегральной функции, тоже даёт табличный интеграл.
Пример 2.1 Вычислим интеграл
В подкоренном выражении выделим полный квадрат:
Делаем замену
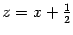
:
В первом из двух интегралов сделаем ещё одну замену,
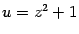
:
Второй интеграл -- табличный:
Продолжая равенство (
2.1) и возвращаясь к исходной переменной

, получаем:
2. Интегралы от произведений синусов и косинусов.
a). Интегралы от произведений синусов и косинусов с разными аргументами, линейно зависящими от  , упрощаются, если применить тригонометрические формулы преобразования произведения в сумму:
, упрощаются, если применить тригонометрические формулы преобразования произведения в сумму:
Пример 2.2 Вычислим интеграл
Преобразуем произведение
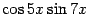
в сумму:
Тогда
б). Расмотрим теперь интегралы вида
где хотя бы одно из чисел
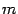
и
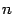
-- нечётное положительное. Такие интегралы вычисляются заменой
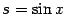
, если нечётна степень косинуса, или
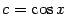
, если нечётна степень синуса. Действительно, пусть
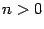
-- нечётное число. Запишем
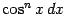
как
а оставшуюся чётную степень косинуса,
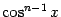
, выразим через синус с помощью формулы
Получим интеграл
После раскрытия скобок этот интеграл легко вычисляется. Аналогично нужно поступать и в случае нечётной степени
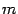
, используя равенство
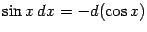
.
Пример 2.3 Найдём интеграл
Отделяя один множитель
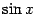
от нечётной степени и объединяя с дифференциалом, получаем:
где
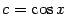
.
в). Заметим, что этот же способ годится и для упрощения интегралов вида
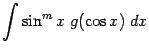
и
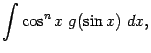
если
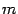
и
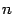
-- нечётные положительные числа.
Пример 2.4 Вычислим интеграл
Отделяя один множитель
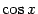
от нечётной степени и объединяя с
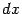
, мы видим, что подынтегральное выражение зависит только от
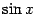
; это означает, что нужно сделать замену
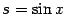
:
Выделим в рациональной дроби
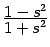
целую часть:
После этого получаем:
г). Рассмотрим теперь случай вычисления интеграла
где оба числа
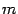
и
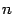
-- чётные неотрицательные.
Такие интегралы упрощаются при помощи тригонометрических формул понижения степени:
Полезна также ещё одна формула понижения степени:
После применения этих формул (быть может, неоднократного) и раскрытия скобок получаются интегралы, в которых степень синуса или косинуса нечётна. Они либо сразу сводятся к табличным линейной заменой, либо их можно вычислить тем способом, что разобран выше, в п. б).
Пример 2.5 Найдём интеграл
Подынтегральную функцию можно преобразовать, понизив степень:
Поэтому
В более сложных случаях преобразовывать подынтегральную функцию можно разными способами и, соответственно, по-разному сводить исходный интеграл к табличным. Следует помнить, однако, что формально различные первообразные на самом деле либо совпадают, либо различаются на постоянное слагаемое. Приведём пример, в котором разные преобразования приводят к несовпадающим ответам.
Пример 2.6 Вычислим интеграл
Заменяем множители подынтегральной функции по формулам:
и получаем:
Мы применили вновь формулу понижения степени для
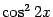
, а также преобразовали произведение
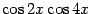
в сумму. Далее получаем:
Другой способ преобразований таков:
Первообразные, стоящие в правых частях формул, тождественно равны друг другу, хотя это видно не сразу. Докажите это при помощи тригономегрических преобразований.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
![]() , где
, где ![]() -- некоторые постоянные, вида
-- некоторые постоянные, вида 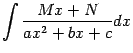 и
и 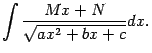
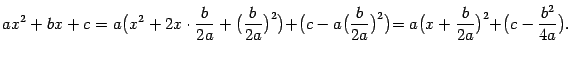
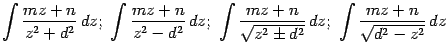
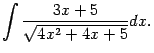
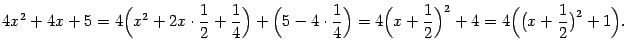
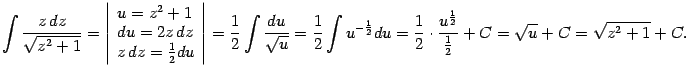
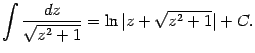
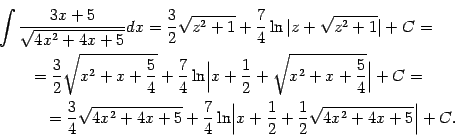
![]() , упрощаются, если применить тригонометрические формулы преобразования произведения в сумму:
, упрощаются, если применить тригонометрические формулы преобразования произведения в сумму: 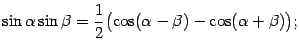
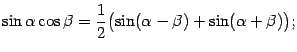
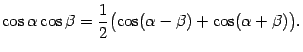
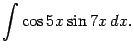
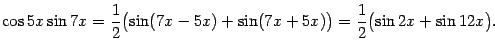
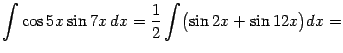
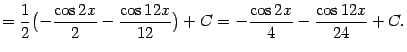
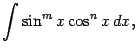
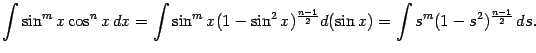
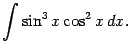
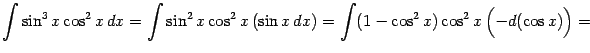
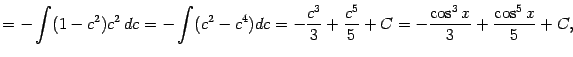
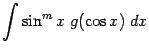 и
и