‹-- Назад
Бесконечно большие величины и бесконечные пределы
для любого, как угодно большого, положительного числа
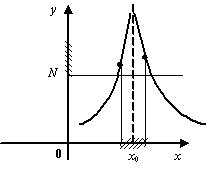
Тогда функция ![]() называется бесконечно большой при базе
называется бесконечно большой при базе ![]() ; это обозначается так:
; это обозначается так:
Если при этом ![]() при
при ![]() , то для положительной бесконечно большой
, то для положительной бесконечно большой ![]() можно писать
можно писать ![]() или
или ![]() , а если
, а если ![]() , то для отрицательной бесконечно большой
, то для отрицательной бесконечно большой ![]() можно писать
можно писать ![]() или
или ![]() .
.
Нужно, конечно, чётко осознавать, что предел, равный бесконечности, -- это чисто условная запись и что в этом случае никакого числового значения такой предел не имеет и, следовательно, не существует, в смысле определения предела функции.
 .
. 
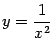
В качестве упражнения найдите зависимость числа ![]() , задающего окончание
, задающего окончание ![]() базы
базы ![]() , от числа
, от числа ![]() .
.
В качестве упражнения найдите зависимость числа ![]() , задающего окончание
, задающего окончание ![]() базы
базы ![]() , от числа
, от числа ![]() .
.
Связь бесконечно больших и бесконечно малых величин устанавливает следующая теорема.
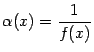 -- бесконечно малая при базе
-- бесконечно малая при базе Доказательство. Для начала заметим, что на всех достаточно далёких окончаниях ![]() базы
базы ![]() будет
будет ![]() , так что функция
, так что функция ![]() определена на этих окончаниях. Далее, пусть взято некоторое
определена на этих окончаниях. Далее, пусть взято некоторое ![]() . Положим
. Положим 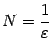 и выберем такое окончание
и выберем такое окончание ![]() , что
, что 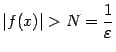 при
при ![]() из этого окончания. Тогда
из этого окончания. Тогда 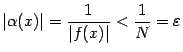 при таких
при таких ![]() , что и означает, что
, что и означает, что ![]() .
.
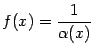 не всегда является бесконечно большой при базе
не всегда является бесконечно большой при базе
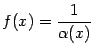 -- бесконечно большая при базе
-- бесконечно большая при базе Докажите эту теорему в качестве упражнения.
Утверждение, что некоторая функция ![]() является бесконечно большой положительной величиной при базе
является бесконечно большой положительной величиной при базе ![]() означает при вычислении пределов, что при замене
означает при вычислении пределов, что при замене ![]() база
база ![]() переходит в базу
переходит в базу ![]() . Если же
. Если же ![]() -- отрицательная бесконечно большая, то после замены получится база
-- отрицательная бесконечно большая, то после замены получится база ![]() . Прослеживая за изменениями баз при последовательных заменах, можно вычислять многие пределы.
. Прослеживая за изменениями баз при последовательных заменах, можно вычислять многие пределы.
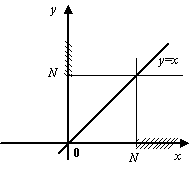
Рассмотрим замену ![]() . При
. При ![]() будет
будет 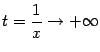 . Пусть теперь
. Пусть теперь ![]() . При
. При ![]() будет
будет ![]() . Наконец, пусть
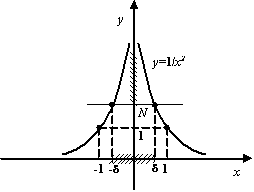
. Наконец, пусть ![]() . При
. При ![]() будет
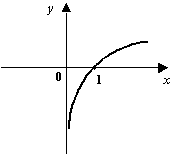
будет ![]() . (См. графики, расположенные ниже.) Последнее соотношение означает, что
. (См. графики, расположенные ниже.) Последнее соотношение означает, что
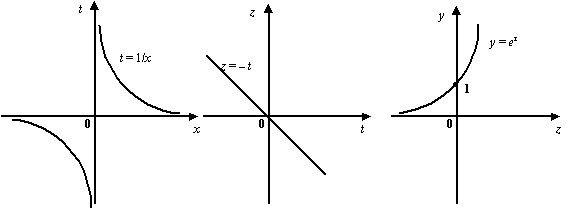
Заметим, что при решении было важно отследить изменение функций именно при ![]() , стремящемся к 0 справа. В качестве упражнения покажите, что если бы рассматривалась база
, стремящемся к 0 справа. В качестве упражнения покажите, что если бы рассматривалась база ![]() , то получилась бы бесконечно большая положительная величина
, то получилась бы бесконечно большая положительная величина ![]() , а при базе
, а при базе ![]() величина
величина ![]() не имеет никакого предела и не является бесконечно большой.
не имеет никакого предела и не является бесконечно большой.