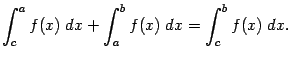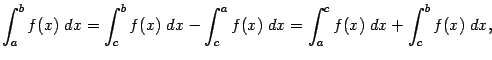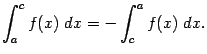‹-- Назад До сих пор мы ограничивались случаями, когда в интеграле 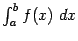 либо
либо 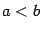 , либо
, либо 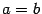 (в последнем случае считали, что интеграл равен 0). Распространим теперь определение на случай произвольных
(в последнем случае считали, что интеграл равен 0). Распространим теперь определение на случай произвольных 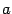 и
и 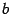 , то есть рассмотрим и случай, когда
, то есть рассмотрим и случай, когда 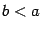 . При этом положим
. При этом положим
Интеграл, стоящий в правой части этого равенства, берётся по отрезку
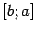
, поскольку
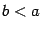
, и поэтому имеет смысл предела интегральных сумм и, в случае непрерывной функции

, может быть вычислен по формуле Ньютона - Лейбница:
Но тогда получаем, что
то есть формула Ньютона - Лейбница сохраняет силу и в случае, когда
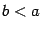
. (Заметим, что при
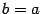
она также верна, поскольку и тогда и
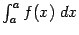
, и разность
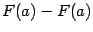
равны 0.)
Упражнение 3.1 Проверьте, что формулы, выражающие линейность интеграла:
и его аддитивность:
сохраняются и в случае произвольного расположения точек
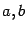
и
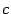
. При этом нужно, разумеется, предполагать интегрируемость функций
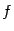
и
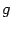
на отрезке, включающем в себя все используемые в формуле точки
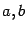
и
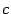
.
Пусть, например, требуется проверить формулу аддитивности при 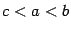 . Тогда, по теореме об аддитивности определённого интеграла, имеем:
. Тогда, по теореме об аддитивности определённого интеграла, имеем:
Отсюда
поскольку, по определению,
Таким образом, формула аддитивности сохраняется при указанном расположении точек
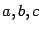
.
Остальные случаи рассмотрите самоcтоятельно.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
![]() либо
либо ![]() , либо
, либо ![]() (в последнем случае считали, что интеграл равен 0). Распространим теперь определение на случай произвольных
(в последнем случае считали, что интеграл равен 0). Распространим теперь определение на случай произвольных ![]() и
и ![]() , то есть рассмотрим и случай, когда
, то есть рассмотрим и случай, когда ![]() . При этом положим
. При этом положим 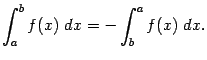
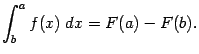
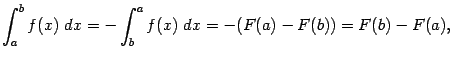
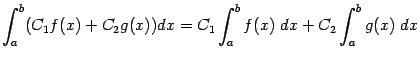
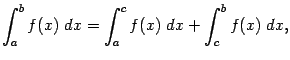
![]() . Тогда, по теореме об аддитивности определённого интеграла, имеем:
. Тогда, по теореме об аддитивности определённого интеграла, имеем: