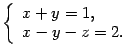‹-- Назад
Основные задачи на прямую и плоскость
Довольно часто встает следующая задача. Требуется от общих уравнений прямой перейти к параметрическим, которые в некотором смысле являются более удобными. Рассмотрим, как решить такую задачу.Для того, чтобы написать параметрические уравнения прямой нужно знать координаты какой-нибудь точки на прямой и координаты направляющего вектора. Как найти координаты точки ![]() на прямой, мы уже обсуждали выше Направляющий вектор можно найти двумя способами.
на прямой, мы уже обсуждали выше Направляющий вектор можно найти двумя способами.
Во-первых, можно найти координаты другой точки ![]() на этой же прямой и в качестве направляющего вектора взять вектор
на этой же прямой и в качестве направляющего вектора взять вектор ![]() .
.
Во-вторых, если заметить, что нормальные векторы ![]() и
и ![]() плоскостей, чьи уравнения образуют систему уравнений для прямой, ортогональны самой прямой, то можно сделать вывод: любой ненулевой вектор, ортогональный векторам
плоскостей, чьи уравнения образуют систему уравнений для прямой, ортогональны самой прямой, то можно сделать вывод: любой ненулевой вектор, ортогональный векторам ![]() и
и ![]() , можно принять в качестве направляющего вектора p. В частности, можно положить
, можно принять в качестве направляющего вектора p. В частности, можно положить ![]() .
.
Требуется написать ее параметрические уравнения.
Решение. Найдем какую-нибудь точку ![]() на прямой. Положим
на прямой. Положим ![]() . Система (11.15) примет вид
. Система (11.15) примет вид
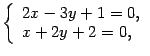
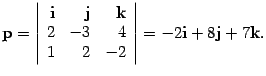
Ответ: 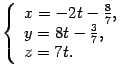
Дано уравнение плоскости и уравнения прямой. Требуется найти их точку пересечения.
Так как точка пересечения принадлежит и прямой, и плоскости, то она удовлетворяет и уравнению плоскости, и уравнениям прямой. Поэтому для решения задачи нужно объединить уравнение плоскости и уравнения прямой в одну систему и решить ее.
Решение. Прямая задана каноническими уравнениями. Им соответствует система уравнений
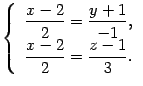
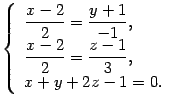
Ответ: ![]() .
.
Следующие две задачи связаны с нахождением угла.
1. Даны уравнения двух прямых. Требуется найти угол между этими прямыми.
Угол ![]() между прямыми -- это угол
между прямыми -- это угол ![]() между их направляющими векторами, если направляющие векторы образуют острый угол
между их направляющими векторами, если направляющие векторы образуют острый угол ![]() , или
, или ![]() , если
, если ![]() -- тупой угол
-- тупой угол ![]() . Во втором случае
. Во втором случае ![]() .
.
Для решения задачи достаточно найти направляющие векторы ![]() и
и ![]() прямых. Тогда
прямых. Тогда
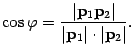
2. Даны уравнение плоскости ![]() и уравнения прямой
и уравнения прямой ![]() . Требуется найти угол
. Требуется найти угол ![]() между прямой и плоскостью.
между прямой и плоскостью.
По определению, угол между прямой и плоскостью -- это угол между прямой и ее проекцией на эту плоскость (рис. 11.12).

Пусть ![]() -- угол между нормальным вектором n плоскости
-- угол между нормальным вектором n плоскости ![]() и направляющим вектором p прямой
и направляющим вектором p прямой ![]() . Тогда либо
. Тогда либо ![]() (рис. 11.12), либо
(рис. 11.12), либо ![]() (рис. 11.13).
(рис. 11.13).

В обоих случаях ![]() , а так как
, а так как ![]() , то
, то
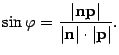
Еще одну, более сложную, задачу рассмотрим при конкретных числовых данных.
Решение. Найдем сначала проекцию

Для этого напишем уравнение плоскости ![]() , проходящей через точку
, проходящей через точку ![]() и перпендикулярной прямой
и перпендикулярной прямой ![]() , а затем найдем точку
, а затем найдем точку ![]() , являющуюся точкой пересечения плоскости и прямой.
, являющуюся точкой пересечения плоскости и прямой.
Заметим, что плоскость, перпендикулярная прямой ![]() , параллельна нормальным векторам
, параллельна нормальным векторам ![]() и
и ![]() плоскостей, соответствующих уравнениям в системе (11.16). Поэтому нормальный вектор n плоскости, перпендикулярной прямой
плоскостей, соответствующих уравнениям в системе (11.16). Поэтому нормальный вектор n плоскости, перпендикулярной прямой ![]() , можно взять равным
, можно взять равным ![]() :
: ![]() ,
, ![]() ,
,
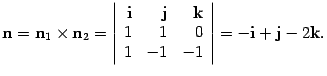
Находим точку ![]() :
:
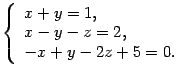
Пусть ![]() -- искомая точка. Тогда из рис. 11.14 видно, что
-- искомая точка. Тогда из рис. 11.14 видно, что ![]() . Находим
. Находим ![]() ,
, ![]() . Тогда
. Тогда
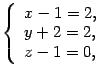
Ответ: ![]() .
.