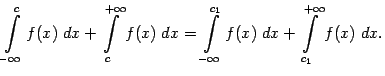‹-- Назад
Несобственные интегралы первого рода
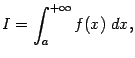
Если же предела ![]() не существует (например, если
не существует (например, если ![]() при
при ![]() ), то интеграл
), то интеграл ![]() называется расходящимся (то есть расходится) и не имеет никакого числового значения.
называется расходящимся (то есть расходится) и не имеет никакого числового значения.
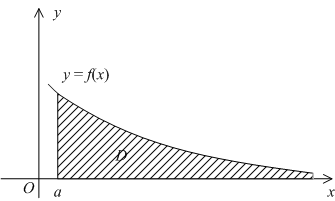
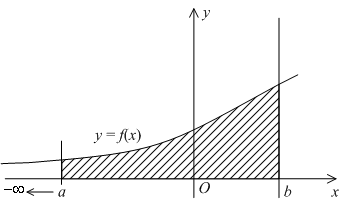
Геометрически, в случае ![]() , величина несобственного интеграла
, величина несобственного интеграла ![]() означает, по определению, площадь бесконечно длинной области
означает, по определению, площадь бесконечно длинной области ![]() , лежащей в координатной плоскости между лучом
, лежащей в координатной плоскости между лучом ![]() на оси
на оси ![]() , графиком
, графиком ![]() и вертикальным отрезком
и вертикальным отрезком ![]() (см. рис.).
(см. рис.).
Сходящиеся интегралы соответствуют таким областям ![]() , площадь которых конечна (хотя сама область
, площадь которых конечна (хотя сама область ![]() неограничена), а расходящиеся (в случае
неограничена), а расходящиеся (в случае ![]() ) -- неограниченным областям с бесконечной площадью. В случае, когда
) -- неограниченным областям с бесконечной площадью. В случае, когда ![]() при
при ![]() , часто пишут формально:
, часто пишут формально:
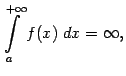
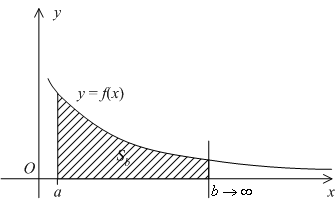
Само определение значения интеграла через предел интегралов по конечным, но увеличивающимся отрезкам означает исчерпание площади ![]() путем учёта все большей её части
путем учёта все большей её части 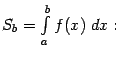 правый вертикальный отрезок, проведённый при
правый вертикальный отрезок, проведённый при ![]() , отодвигается всё дальше и дальше в бесконечность; в пределе будет учтена вся площадь под графиком
, отодвигается всё дальше и дальше в бесконечность; в пределе будет учтена вся площадь под графиком ![]() (см. рис.).
(см. рис.).
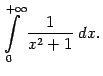
Согласно определению, нам нужно вычислить значение функции
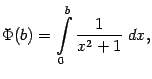
Итак,
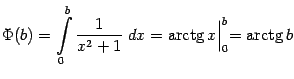
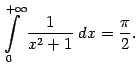
Заметим, что тем самым мы вычислили площадь бесконечно длинной области под графиком ![]() , лежащей над положительной полуосью (см. рис.).
, лежащей над положительной полуосью (см. рис.).
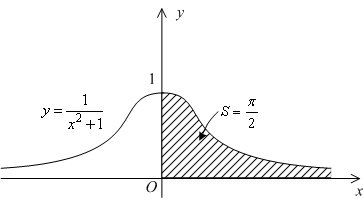
Поскольку рассматриваемая функция
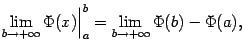
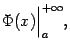
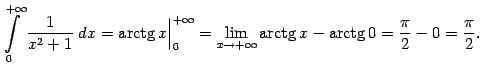
Ниже мы часто будем прибегать к такой укороченной записи.
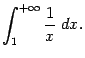
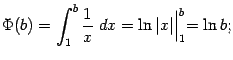
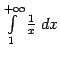 расходится и, следовательно, не имеет никакого числового значения.
расходится и, следовательно, не имеет никакого числового значения. 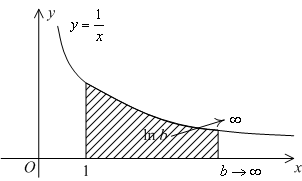
Геометрически это означает, что площадь под графиком
Аналогично случаю интегрирования по промежутку ![]() , уходящему в
, уходящему в ![]() , рассматривается и случай, когда область интегрирования простирается в
, рассматривается и случай, когда область интегрирования простирается в ![]() . Дадим в этом случае такое определение:
. Дадим в этом случае такое определение:
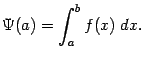
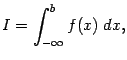
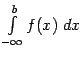 называется сходящимся (то есть сходится). Если же предела
называется сходящимся (то есть сходится). Если же предела 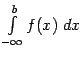 называется расходящимся (то есть расходится) и не имеет никакого числового значения.
называется расходящимся (то есть расходится) и не имеет никакого числового значения. Геометрически, в случае неотрицательной подынтегральной функции ![]() , вычисление несобственного интеграла
, вычисление несобственного интеграла 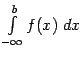 означает нахождение площади бесконечно длинной области
означает нахождение площади бесконечно длинной области ![]() , лежащей между осью
, лежащей между осью ![]() и графиком
и графиком ![]() , левее вертикальной линии
, левее вертикальной линии ![]() . Условие
. Условие ![]() означает, что мы исчерпываем всю площадь, отодвигая всё левее, "в минус бесконечность", линию
означает, что мы исчерпываем всю площадь, отодвигая всё левее, "в минус бесконечность", линию ![]() , временно ограничивающую рассматриваемую часть области справа (см. рис.).
, временно ограничивающую рассматриваемую часть области справа (см. рис.).
В интегралах
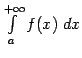 и
и 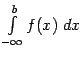 знаки
знаки Очевидно, что при изменении направления на оси ![]() , то есть при замене
, то есть при замене ![]() , интеграл
, интеграл 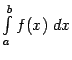 переходит в равный ему интеграл
переходит в равный ему интеграл 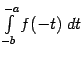 и, соответственно, после перехода к пределу, несобственный интеграл
и, соответственно, после перехода к пределу, несобственный интеграл 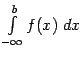 переходит в равный ему интеграл
переходит в равный ему интеграл 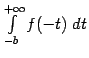 . Таким образом, все свойства интегралов по промежутку
. Таким образом, все свойства интегралов по промежутку ![]() повторяют соответствующие свойства интегралов по промежутку
повторяют соответствующие свойства интегралов по промежутку ![]() , изучением которых можно и ограничиться. Так мы далее и поступим, не разбирая отдельно свойств интегралов вида
, изучением которых можно и ограничиться. Так мы далее и поступим, не разбирая отдельно свойств интегралов вида 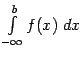 .
.
Наконец, дадим определение интегралу от функции, заданной на всей числовой оси.
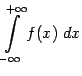
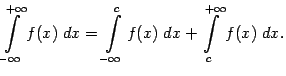
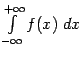 считается сходящимся, а если хотя бы один из них расходится (при этом неважно, сходится или расходится другой), то и интеграл
считается сходящимся, а если хотя бы один из них расходится (при этом неважно, сходится или расходится другой), то и интеграл 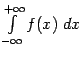 считается расходящимся (тогда он не имеет никакого числового значения).
считается расходящимся (тогда он не имеет никакого числового значения). Заметим, что в точности в соответствии с этим определением мы поступили выше, когда определяли площадь области, расположенной под всем графиком функции ![]() ; эта площадь оказалась равной числу
; эта площадь оказалась равной числу ![]() .
.
Для корректности данного определения интеграла по всей оси нам следует доказать, что результат не зависит от выбора точки ![]() , то есть при выборе двух разных точек
, то есть при выборе двух разных точек ![]() и
и ![]() определение даёт одно и то же, поскольку
определение даёт одно и то же, поскольку
Действительно, пусть
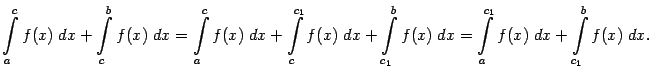
В дальнейшем для облегчения записи того, сходится или расходится несобственный интеграл, мы будем использовать следующие обозначения. Тот факт, что интеграл 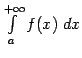 сходится, будем записывать в виде такого неравенства:
сходится, будем записывать в виде такого неравенства:
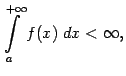
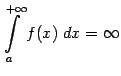
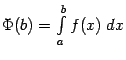 не стремится к
не стремится к 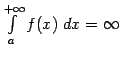 отвечает тому факту, что соответствующая область под графиком функции имеет бесконечную площадь.
отвечает тому факту, что соответствующая область под графиком функции имеет бесконечную площадь. Аналогичные обозначения мы будем применять и для интегралов по промежуткам вида ![]() и по всей оси, а также, в дальнейшем, и для несобственных интегралов второго рода (от неограниченных функций).
и по всей оси, а также, в дальнейшем, и для несобственных интегралов второго рода (от неограниченных функций).