‹-- Назад
Определение непрерывности функции
Мы повторим здесь определение непрерывности функции, данное выше, в главе о пределах.
определена на некотором интервале 
, для которого 
-- внутренняя точка. Функция называется непрерывной в точке , если существует предел при 
и этот предел равен значению 
, то есть 
Пусть функция определена на некотором полуинтервале 
, для которого -- левый конец. Функция называется непрерывной справа в точке , если существует предел при 
и этот предел равен значению , то есть
Пусть, наконец, функция определена на некотором полуинтервале 
, для которого -- правый конец. Функция называется непрерывной слева в точке , если существует предел при 
и этот предел равен значению , то есть
Из теоремы о связи двустороннего предела с односторонними (теорема 2.1) сразу следует, как уже отмечалось в главе 2, что имеет место следующее предложение.
тогда и только тогда непрерывна в точке , когда она непрерывна в точке справа и слева, то есть когда выполнены следующие условия: 1) функция определена в точке и в некоторой окрестности этой точки;
2) существует предел значений функции слева: 
;
3) существует предел значений функции справа: 
;
4) эти два предела совпадают между собой и со значением функции в точке : 
.
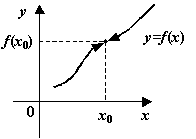
Точка , в которой функция непрерывна, называется точкой непрерывности функции ; так же определяются точки непрерывности слева и справа.
и 
. Тогда 
и 
. Эти значения совпадают, значит, функция 
непрерывна в точке . (Функция 
-- элементарная функция; -- точка её области определения 
. Все элементарные функции непрерывны во всех внутренних точках своих областей определения, в том числе и эта. Так что в этом примере можно было бы заменить любой элементарной функцией, а -- любой внутренней точкой области 
, и вывод остался бы тем же.)
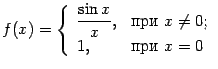и точку 
. При 
функция задаётся формулой 
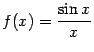, при этом имеем 
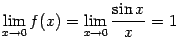(первый замечательный предел). Это значение совпадает с тем, которое задано при 
: 
. Итак, 
, что означает непрервыность функции при . Тем, кто внимательно изучил данное в главе 2 общее понятие базы предела, можно предложить продумать и доказать следующее утверждение:
-- база непроколотых окрестностей точки , окончаниями которой служат интервалы 
, 
; 
-- база непроколотых левых окрестностей точки , окончаниями которой служат полуинтервалы 
, ; 
-- база непроколотых правых окрестностей точки , окончаниями которой служат полуинтервалы 
, . Тогда непрерывность функции в точке эквивалентна тому, что существует предел 
; непрерывность слева в точке -- тому, что существует предел 
; непрерывность справа в точке -- тому, что существует предел 
.
