‹-- Назад Поскольку точки

непрерывности функции

задаются условием
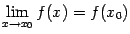
, то часть свойств функций, непрерывных в точке

, следует непосредственно из свойств пределов. Сформулируем их в виде следующей теоремы.
Теорема 3.1 Пусть функции  и
и 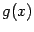 непрерывны в точке
непрерывны в точке  . Тогда функции
. Тогда функции 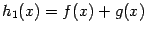 ,
, 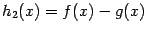 ,
, 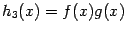 непрерывны в точке
непрерывны в точке  . Если
. Если 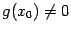 , то функция
, то функция 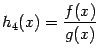 также непрерывна в точке
также непрерывна в точке  .
. Доказательство. Оно сразу же следует из теорем о пределах 2.8, 2.9, 2.10 и следствия 2.5.
Как непосредственное следствие этой теоремы получается следующее
Предложение 3.3 Рассмотрим множество всех функций, определённых в некоторой фиксированной окрестности 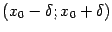 точки
точки  и непрерывных в этой точке. Тогда это множество
и непрерывных в этой точке. Тогда это множество 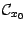 является линейным пространством, то есть замкнуто относительно сложения и умножения на постоянные:
является линейным пространством, то есть замкнуто относительно сложения и умножения на постоянные: Доказательство. Действительно, постоянные 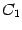 и
и 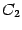 -- это непpеpывные функции (в любой точке); по пpедыдущей теоpеме тогда непpеpывны в точке
-- это непpеpывные функции (в любой точке); по пpедыдущей теоpеме тогда непpеpывны в точке  пpоизведения
пpоизведения 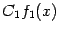 и
и 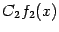 . Но тогда по этой же теоpеме непpеpывна в точке
. Но тогда по этой же теоpеме непpеpывна в точке  и сумма
и сумма 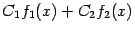 .
.
Теорема 3.2 Пусть функции  и
и 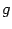 таковы, что существует композиция
таковы, что существует композиция 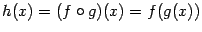 ,
, 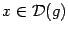 . Пусть функция
. Пусть функция 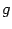 непрерывна в точке
непрерывна в точке 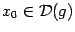 , а функция
, а функция  непрерывна в соответствующей точке
непрерывна в соответствующей точке 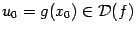 . Тогда композиция
. Тогда композиция 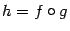 непрерывна в точке
непрерывна в точке  .
. Доказательство. Заметим, что равенство 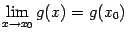 означает, что при
означает, что при 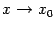 будет
будет 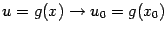 . Значит,
. Значит,
(последнее равенство следует из непрерывности функции

в точке
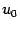
). Значит,
а это равенство означает, что композиция
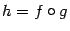
непрерывна в точке

.
Заметим, что, очевидно, в предыдущих двух теоремах можно было бы заменить базу 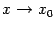 на односторонние базы
на односторонние базы 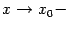 или
или 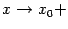 и получить аналогичные утверждения для непрерывности слева или справа:
и получить аналогичные утверждения для непрерывности слева или справа:
Теорема 3.3 Пусть функции  и
и 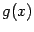 непрерывны слева (справа) в точке
непрерывны слева (справа) в точке  . Тогда функции
. Тогда функции 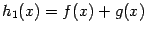 ,
, 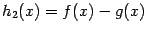 ,
, 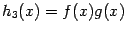 непрерывны слева (соотв. справа) в точке
непрерывны слева (соотв. справа) в точке  . Если
. Если 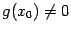 , то функция
, то функция 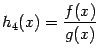 также непрерывна слева (спpава) в точке
также непрерывна слева (спpава) в точке  .
.
Теорема 3.4 Пусть функция 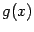 непрерывна слева (справа) в точке
непрерывна слева (справа) в точке  , а функция
, а функция 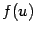 непрерывна в точке
непрерывна в точке 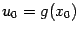 . Тогда композиция
. Тогда композиция 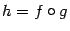 непрерывна слева (соотв. справа) в точке
непрерывна слева (соотв. справа) в точке  .
.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
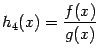 также непрерывна в точке
также непрерывна в точке ![]() и
и ![]() -- это непpеpывные функции (в любой точке); по пpедыдущей теоpеме тогда непpеpывны в точке
-- это непpеpывные функции (в любой точке); по пpедыдущей теоpеме тогда непpеpывны в точке ![]() пpоизведения
пpоизведения ![]() и
и ![]() . Но тогда по этой же теоpеме непpеpывна в точке
. Но тогда по этой же теоpеме непpеpывна в точке ![]() и сумма
и сумма ![]() .
. ![]() означает, что при
означает, что при ![]() будет
будет ![]() . Значит,
. Значит, ![]() на односторонние базы
на односторонние базы ![]() или
или ![]() и получить аналогичные утверждения для непрерывности слева или справа:
и получить аналогичные утверждения для непрерывности слева или справа: 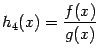 также непрерывна слева (спpава) в точке
также непрерывна слева (спpава) в точке