‹-- Назад
Равномерная непрерывность
Напомним, что непрерывность функцииТем самым непрерывность функции
При этом мы имеем право выбирать число
Предположим теперь, что число ![]() можно выбрать общим для всех
можно выбрать общим для всех ![]() (но, конечно, зависящим от
(но, конечно, зависящим от ![]() ). Тогда говорят, что свойство функции быть непрерывной в точке
). Тогда говорят, что свойство функции быть непрерывной в точке ![]() выполнено равномерно по
выполнено равномерно по ![]() .
.
Дадим теперь такое
Приведём пример равномерно непрерывной функции.
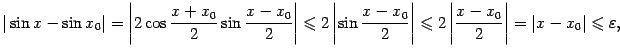 |
так как, во-первых,
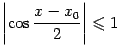 при всех
при всех Лучше изучить условие равномерности по ![]() мы сможем, приведя пример, где оно нарушается.
мы сможем, приведя пример, где оно нарушается.
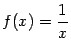 рассматривается на интервале
рассматривается на интервале 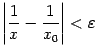 при всех
при всех 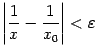 относительно
относительно 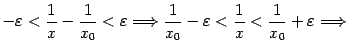 | |
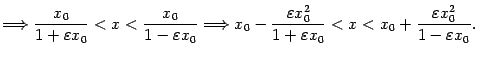 |
Из чисел
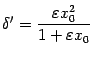 и
и 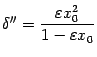 выберем минимальное:
выберем минимальное: 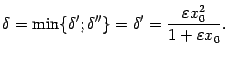
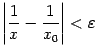 . Проанализируем, однако, зависимость
. Проанализируем, однако, зависимость 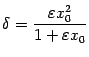 будут убывать и стремиться к 0 (при неизменном значении
будут убывать и стремиться к 0 (при неизменном значении 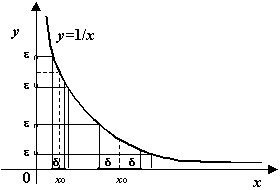
При приближении точки ![]() к началу координат нам приходится по одному и тому же
к началу координат нам приходится по одному и тому же ![]() выбирать всё меньшие
выбирать всё меньшие ![]() -окрестности точки
-окрестности точки ![]() , чтобы обеспечить выполнение неравенства
, чтобы обеспечить выполнение неравенства 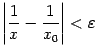 . Выбрать
. Выбрать ![]() общим для всех
общим для всех ![]() , очевидно, невозможно: при заданном
, очевидно, невозможно: при заданном ![]() какое бы фиксированное число
какое бы фиксированное число ![]() ни было взято, мы можем поместить точку
ни было взято, мы можем поместить точку ![]() так близко от 0, что значения
так близко от 0, что значения ![]() и
и ![]() будут отличаться друг от друга больше, чем на
будут отличаться друг от друга больше, чем на ![]() , хотя
, хотя ![]() . Это означает, что функция
. Это означает, что функция 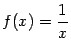 не является равномерно непрерывной на интервале
не является равномерно непрерывной на интервале ![]() .
.
Доказательство этой теоремы достаточно сложно и основывается на тонких свойствах системы действительных чисел, а именно, на том, что любой замкнутый отрезок ![]() является компактом9. Мы пропускаем здесь доказательство теоремы, отсылая за ним заинтересованного читателя к подробным курсам математического анализа, например, Никольский С.М., Курс математического анализа, т. 1. -- М.: Наука, 1991; Фихтенгольц Г.М., Курс дифференциального и интегрального исчисления, т. 1. -- М.-Л.: ГИТТЛ, 1948 и др. годы изд.
является компактом9. Мы пропускаем здесь доказательство теоремы, отсылая за ним заинтересованного читателя к подробным курсам математического анализа, например, Никольский С.М., Курс математического анализа, т. 1. -- М.: Наука, 1991; Фихтенгольц Г.М., Курс дифференциального и интегрального исчисления, т. 1. -- М.-Л.: ГИТТЛ, 1948 и др. годы изд.
В качестве следствия равномерной непрерывности легко получается утверждение теоремы 3.8, а именно,
Приведём это доказательство (хотя теорема 3.8 была ранее доказана другим способом):
Доказательство. Фиксируем какое-либо число ![]() , например
, например ![]() , и выберем
, и выберем ![]() такое, что при всех
такое, что при всех ![]() , для которых
, для которых ![]() , будет
, будет ![]() . Разобьём
. Разобьём ![]() на отрезки длины
на отрезки длины ![]() :
:
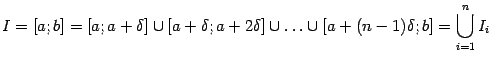
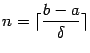 ;10 длина последнего отрезка может оказаться меньше
;10 длина последнего отрезка может оказаться меньше 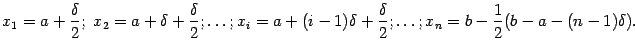
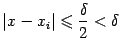 и, следовательно,
и, следовательно,