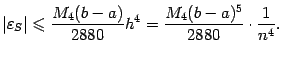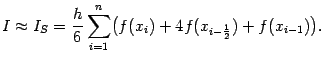‹-- Назад При выводе двух предыдущих квадратурных формул мы приближали график подынтегральной функции

на каждом из отрезков разбиения
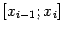
прямой линией: либо касательной в формуле центральных прямоугольников, либо хордой в формуле трапеций. Очередным по сложности шагом является выбор приближения графика функции

в виде параболы -- графика некоторого квадратного трёхчлена
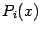
. Его вид, конечно, будет зависеть от отрезка
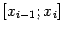
, на котором мы выбираем приближение.
Выберем, например, такой квадратный трёхчлен 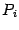 , чтобы его значения в точках
, чтобы его значения в точках 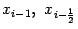 и
и 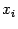 совпадали со значениями функции
совпадали со значениями функции  в этих же точках:
в этих же точках:
Напомним, что через
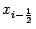
мы обозначали середину отрезка
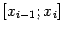
, то есть
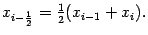
Функцию можно записать в виде
действительно, раскрыв скобки, получим некоторый квадратный трёхчлен. Подберём числа
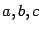
так, чтобы выполнялись равенства (
5.3). Положим
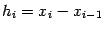
, тогда
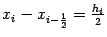
и
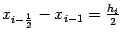
. Подставим
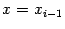
в выражение для
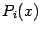
и получим:
то есть
Подстановка
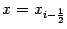
даёт
откуда
Наконец, подставим
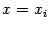
и получим
откуда
Вычислим теперь интеграл от интерполяционной функции 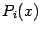 , для чего сделаем в нём замену
, для чего сделаем в нём замену 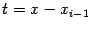 :
:
Осталось просуммировать эти величины по всем отрезкам разбиения. При этом получаем квадратурную формулу, которая называется
формулой Симпсона, или
формулой парабол:
Нетрудно видеть, что это в точности та же "комбинированная" квадратурная формула (
5.2), которую мы получили выше из формул центральных прямоугольников и трапеций.
Замечание 5.1 При вычислении очередного слагаемого
требуется вычислить только два (а не три) новых значения функции

, а именно, значения
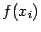
и
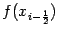
. Значение
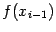
использовалось на предыдущем шаге и было тогда уже вычислено.
Если при применении формулы Симпсона взять все отрезки разбиения одинаковой длины 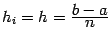 , то формула Симпсона получает вид
, то формула Симпсона получает вид
Раскрыв скобки и объединив одинаковые слагаемые, можно легко привести эту формулу к виду
Действительно, слагаемые с целыми номерами (кроме
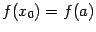
и
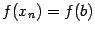
) входят по одному разу в каждое их двух соседних слагаемых в сумме (
5.4), так что для них получается сумма с коэффициентом 2.
Оценка ошибки формулы Симпсона, то есть величины 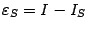 , такова. Предположим, что функция
, такова. Предположим, что функция  имеет на отрезке
имеет на отрезке 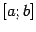 непрерывную четвёртую производную
непрерывную четвёртую производную 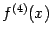 , причём
, причём
при всех
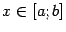
. Тогда при выборе постоянного шага
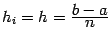
имеет место неравенство
Таким образом, формула Симпсона -- это квадратурная формула
четвёртого порядка точности. Это означает, что при уменьшении шага
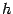
вдвое ошибка
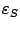
уменьшится примерно в
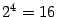
раз, а при уменьшении шага в 10 раз ошибка уменьшится примерно в
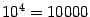
раз.
Доказательство приведённой оценки для формулы Симпсона можно найти, например, в книге
Бахвалов Н. С., Жидков Н. П., Кобельков Г. М. Численные методы. -- М.: Наука, 1987.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
![]() , чтобы его значения в точках
, чтобы его значения в точках ![]() и
и ![]() совпадали со значениями функции
совпадали со значениями функции ![]() в этих же точках:
в этих же точках: 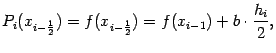
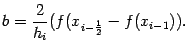
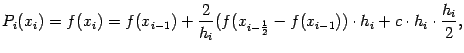
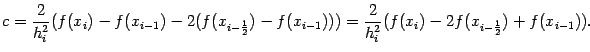
![]() , для чего сделаем в нём замену
, для чего сделаем в нём замену ![]() :
: 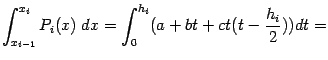
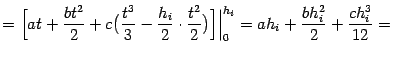
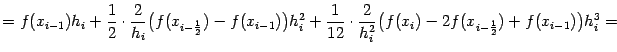
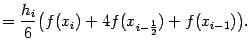
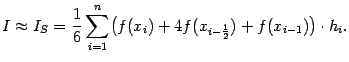
![]() , то формула Симпсона получает вид
, то формула Симпсона получает вид 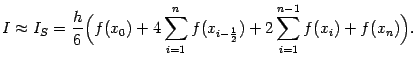
![]() , такова. Предположим, что функция
, такова. Предположим, что функция ![]() имеет на отрезке
имеет на отрезке ![]() непрерывную четвёртую производную
непрерывную четвёртую производную ![]() , причём
, причём