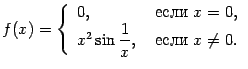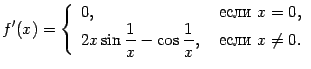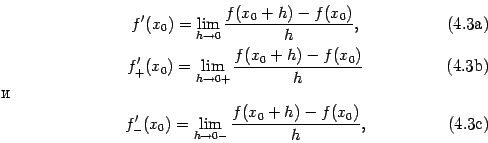при этом в формуле (4.3a) функция должна быть определена на некотором интервале 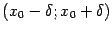 , в формуле (4.3b) -- на некотором полуинтервале
, в формуле (4.3b) -- на некотором полуинтервале 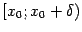 , а в формуле (4.3c) -- на некотором полуинтервале
, а в формуле (4.3c) -- на некотором полуинтервале 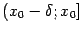 .
. Функция, имеющая в точке  производную (соотв. левую производную, правую производную), называется дифференцируемой (соотв. дифференцируемой слева, дифференцируемой справа) в точке
производную (соотв. левую производную, правую производную), называется дифференцируемой (соотв. дифференцируемой слева, дифференцируемой справа) в точке  . Функция, дифференцируемая во всех точках некоторого интервала
. Функция, дифференцируемая во всех точках некоторого интервала 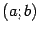 , называется дифференцируемой на интервале
, называется дифференцируемой на интервале 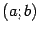 . Пусть теперь
. Пусть теперь 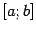 -- замкнутый отрезок. Функция, дифференцируемая во всех точках интервала
-- замкнутый отрезок. Функция, дифференцируемая во всех точках интервала 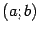 , дифференцируемая справа в точке
, дифференцируемая справа в точке 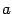 и дифференцируемая слева в точке
и дифференцируемая слева в точке 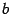 , называется дифференцируемой на отрезке
, называется дифференцируемой на отрезке 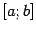 .
.
Вычислим производную данной функции  в различных точках
в различных точках 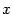 некоторого интервала
некоторого интервала 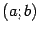 и предположим, что производная
и предположим, что производная 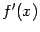 существует при всех
существует при всех 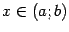 . Тогда мы можем задать соответствие между точками
. Тогда мы можем задать соответствие между точками 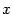 интервала и числами
интервала и числами 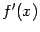 и получаем функцию
и получаем функцию 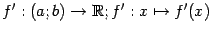 . Эта функция
. Эта функция 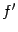 называется производной от функции
называется производной от функции 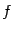 (или первой производной от
(или первой производной от 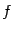 ).
).
С математической точки зрения, разница между формулами (4.3 a-c) невелика: согласно теореме о связи двустороннего предела с односторонними, если существует производная 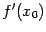 , то существуют обе односторонние производные (правая
, то существуют обе односторонние производные (правая 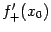 и левая
и левая 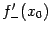 ), и
), и 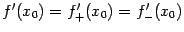 . Обратно, если существуют и равны друг другу односторонние производные,
. Обратно, если существуют и равны друг другу односторонние производные, 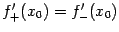 , то существует и производная
, то существует и производная 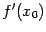 , совпадающая с их общим значением.
, совпадающая с их общим значением.
В предположении, что производная 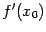 существует, мы можем теперь сказать, что число
существует, мы можем теперь сказать, что число 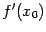 задаёт мгновенную скорость изменения координаты
задаёт мгновенную скорость изменения координаты 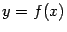 при
при 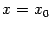 ; с геометрической точки зрения, эта скорость равна тангенсу угла наклона касательной, проведённой к графику
; с геометрической точки зрения, эта скорость равна тангенсу угла наклона касательной, проведённой к графику 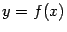 при
при 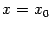 : чем быстрее растут (или убывают) значения функции, тем круче наклонён график к оси
: чем быстрее растут (или убывают) значения функции, тем круче наклонён график к оси 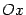 (составляя, соответственно, положительный или отрицательный угол с осью
(составляя, соответственно, положительный или отрицательный угол с осью 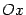 ).
).
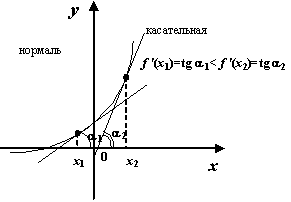
Рис.4.3.Скорость роста значений функции соответствует величине тангенса угла наклона касательной
Замечание 4.1 В числителе дроби, предельное значение которой даёт производную, стоит выражение
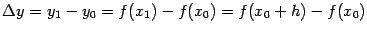
. Оно называется
приращением функции. В знаменателе стоит величина
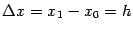
. Она называется
приращением аргумента. Величина
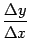
называется
разностным отношением12. Условие
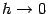
можно, очевидно, записать в виде
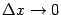
(кстати, база
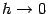
эквивалентна базе
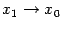
). Тем самым определение производной можно записать в таком виде:
От такой записи происходит обозначение производной в виде
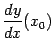
.
Пример 4.1 Рассмотрим линейную функцию
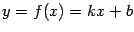
. Тогда
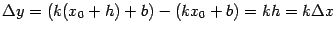
,
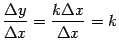
и
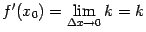
при любом

. Получаем, что для линейной функции производная в любой точке равна угловому коэффициенту
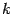
. (Что неудивительно: ведь касательная к прямой, служащей графиком линейной функции, -- это та же самая прямая, а угловой коэффициент касательной равен производной!) В частности, при
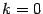
получаем, что производная любой постоянной, то есть функции
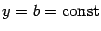
, равна 0:
а при
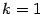
и
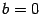
получаем, что
Пример 4.2 Пусть
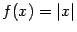
и
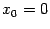
. Вычислим односторонние производные
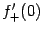
и
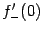
.
При 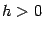 имеем
имеем 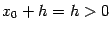 и
и 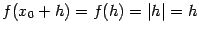 . Значит, разностное отношение равно
. Значит, разностное отношение равно 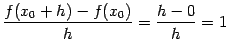 и
и 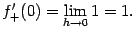
При 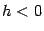 имеем
имеем 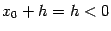 и
и 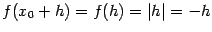 . Значит, разностное отношение равно
. Значит, разностное отношение равно 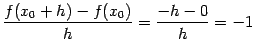 и
и 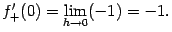
Графически это означает следующее. Мы строим касательную к графику
в точке
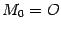
, сначала пользуясь секущими
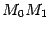
с точкой
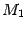
правее
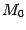
. Эта касательная, как и все такие секущие, совпадают между собой и имеют уравнение
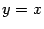
, задающее прямую, наклонённую под углом
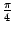
к оси
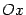
(
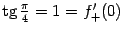
). Далее, мы строим касательную, пользуясь секущими
с точкой
левее
. Все такие секущие и касательная, по ним построенная, совпадают между собой и имеют уравнение
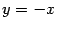
, задающее прямую, наклонённую под углом
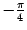
к оси
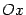
(
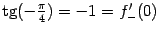
).
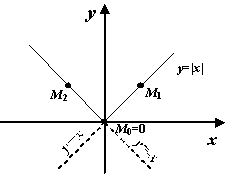
Рис.4.4.График 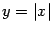 имеет излом при
имеет излом при 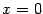
Таким образом, неравенство левой и правой производной выражает тот геометрический факт, что линия 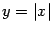 имеет при
имеет при 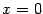 излом под углом
излом под углом 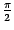 и не имеет общей касательной сразу к двум сторонам этого угла.
и не имеет общей касательной сразу к двум сторонам этого угла.
Покажем теперь, что дифференцируемая функция не может быть разрывной.
Теорема 4.1 Пусть функция  дифференцируема (дифференцируема слева, дифференцируема справа) в точке
дифференцируема (дифференцируема слева, дифференцируема справа) в точке  . Тогда
. Тогда  непрерывна (соотв. непрерывна слева, непрерывна справа) в этой точке
непрерывна (соотв. непрерывна слева, непрерывна справа) в этой точке  .
. Доказательство. Из существования производной
следует, что
откуда что и означает непрерывность функции  в точке
в точке  .
. Для доказательства теоремы в случае существования односторонних производных достаточно сменить базу 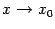 на базу
на базу 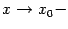 или
или 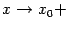 .
.
Замечание 4.2 Предыдущий пример показывает, что обратное утверждение неверно: функция не обязательно имеет производную во всех тех точках, где она непрерывна. Действительно, функция
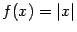
непрерывна при
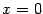
, но не имеет производной в точке 0.
Более того, можно построить пример такой функции, которая непрерывна во всех точках числовой прямой, но не имеет производной ни в одной из этих точек. Два таких примера (функции Вейерштрасса и Ван дер Вардена) приведены в весьма любопытной и полезной для понимания математики книге [Гелбаум Б., Олмстед Дж., Контрпримеры в анализе. -- М.: Мир, 1967. -- С. 52 - 53]. Построение функции Вейерштрасса приведено также в учебнике [Калугина Т.Ф., Киселёв В.Ю., Математический анализ. -- Иваново, изд. ИГАСА, 1997. -- С. 99 -101]. (Функция Вейерштрасса обладает ещё следующим замечательным свойством: она не монотонна ни на каком, как угодно коротком, интервале.) Построение непрерывных, но нигде не дифференцируемых функций -- довольно сложная процедура.
Замечание 4.3 Заметим, что доказанная теорема гарантирует непрерывность функции, имеющей производную в точке

, только в этой самой точке

, но не на некотором интервале, окружающем

. Примером функции, имеющей производную при
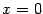
, но разрывной при всех
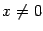
, служит функция
(Напомним, что через
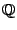
обозначается множество всех рациональных чисел. Рациональные числа, как и иррациональные, плотно расположены на числовой оси
: между любыми двумя рациональными числами найдётся иррациональное число, а между двумя иррациональными -- рациональное.) Действительно,
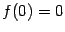
; если
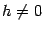
-- рациональное число, то разностное отношение
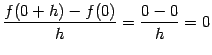
, а если
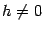
-- иррациональное, то
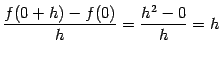
. И в том, и в другом случае разностное отношение стремится к 0 при
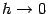
, так что существует производная
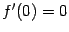
. Однако, как нетрудно заметить, функция

разрывна во всех точках
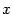
, кроме
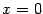
.
Замечание 4.4 Заметим также, что даже если функция имеет производную на некотором интервале, окружающем точку

, значение
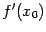
может оказаться не равным пределу значений
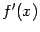
при
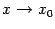
, то есть производная
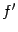
может оказаться разрывной функцией.
13 Примером такой функции с всюду существующей, но разрывной производной
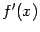
может служить функция
Производная этой функции, как мы покажем ниже, равна
Нетрудно видеть, что эта функция имеет разрыв второго рода в точке 0, из-за слагаемого
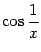
, совершающего бесконечное число колебаний амплитуды 1 в любой, как угодно малой, окрестности точки 0.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
![]() производную (соотв. левую производную, правую производную), называется дифференцируемой (соотв. дифференцируемой слева, дифференцируемой справа) в точке
производную (соотв. левую производную, правую производную), называется дифференцируемой (соотв. дифференцируемой слева, дифференцируемой справа) в точке ![]() . Функция, дифференцируемая во всех точках некоторого интервала
. Функция, дифференцируемая во всех точках некоторого интервала ![]() , называется дифференцируемой на интервале
, называется дифференцируемой на интервале ![]() . Пусть теперь
. Пусть теперь ![]() -- замкнутый отрезок. Функция, дифференцируемая во всех точках интервала
-- замкнутый отрезок. Функция, дифференцируемая во всех точках интервала ![]() , дифференцируемая справа в точке
, дифференцируемая справа в точке ![]() и дифференцируемая слева в точке
и дифференцируемая слева в точке ![]() , называется дифференцируемой на отрезке
, называется дифференцируемой на отрезке ![]() .
. ![]() в различных точках
в различных точках ![]() некоторого интервала
некоторого интервала ![]() и предположим, что производная
и предположим, что производная ![]() существует при всех
существует при всех ![]() . Тогда мы можем задать соответствие между точками
. Тогда мы можем задать соответствие между точками ![]() интервала и числами
интервала и числами ![]() и получаем функцию
и получаем функцию ![]() . Эта функция
. Эта функция ![]() называется производной от функции
называется производной от функции ![]() (или первой производной от
(или первой производной от ![]() ).
). ![]() , то существуют обе односторонние производные (правая
, то существуют обе односторонние производные (правая ![]() и левая
и левая ![]() ), и
), и ![]() . Обратно, если существуют и равны друг другу односторонние производные,
. Обратно, если существуют и равны друг другу односторонние производные, ![]() , то существует и производная
, то существует и производная ![]() , совпадающая с их общим значением.
, совпадающая с их общим значением. ![]() существует, мы можем теперь сказать, что число
существует, мы можем теперь сказать, что число ![]() задаёт мгновенную скорость изменения координаты
задаёт мгновенную скорость изменения координаты ![]() при
при ![]() ; с геометрической точки зрения, эта скорость равна тангенсу угла наклона касательной, проведённой к графику
; с геометрической точки зрения, эта скорость равна тангенсу угла наклона касательной, проведённой к графику ![]() при
при ![]() : чем быстрее растут (или убывают) значения функции, тем круче наклонён график к оси
: чем быстрее растут (или убывают) значения функции, тем круче наклонён график к оси ![]() (составляя, соответственно, положительный или отрицательный угол с осью
(составляя, соответственно, положительный или отрицательный угол с осью ![]() ).
). 
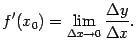
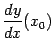 .
. 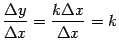 и
и ![]() имеем
имеем ![]() и
и ![]() . Значит, разностное отношение равно
. Значит, разностное отношение равно 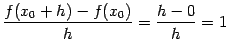 и
и ![]()
![]() имеем
имеем ![]() и
и ![]() . Значит, разностное отношение равно
. Значит, разностное отношение равно 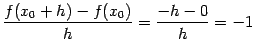 и
и ![]()
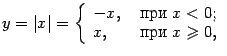

![]() имеет при
имеет при ![]() излом под углом
излом под углом ![]() и не имеет общей касательной сразу к двум сторонам этого угла.
и не имеет общей касательной сразу к двум сторонам этого угла. 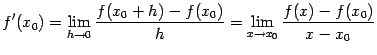
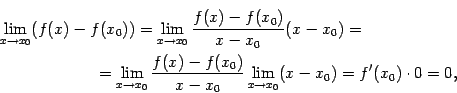
![]() на базу
на базу ![]() или
или ![]() .
. 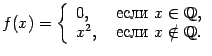
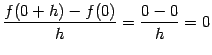 , а если
, а если 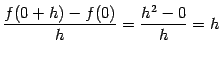 . И в том, и в другом случае разностное отношение стремится к 0 при
. И в том, и в другом случае разностное отношение стремится к 0 при