‹-- Назад Дальнейшее повышение порядка точности формул, подобных квадратурным формулам центральных прямоугольников, трапеций, парабол, можно получить, применяя на отрезках разбиения интерполяцию функции

многочленами более высокой степени (ниже мы использовали линейные функции, то есть многочлены степени 1, и квадратные трёхчлены -- многочлены степени 2).
Например, если использовать кубическое интерполирование, то есть приближать функцию  многочленами степени 3, то получится формула, называемая кквадратурной формулой
многочленами степени 3, то получится формула, называемая кквадратурной формулой 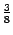 (три восьмых)":
(три восьмых)":
где
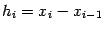
,
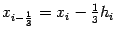
и
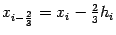
, то есть точки
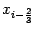
и
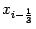
делят отрезок разбиения
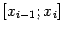
на три равных части. Число
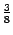
в названии формулы связано с тем, что если положить
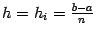
постоянным и ввести обозначение
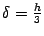
, то формула получает вид
Если же использовать для интерполяции многочлены шестой степени 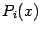 и заменять интеграл ог
и заменять интеграл ог  на каждом из отрезков
на каждом из отрезков 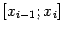 на интеграл от
на интеграл от 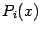 , то получится квадратурная формула, называемая формулой Уэддля:
, то получится квадратурная формула, называемая формулой Уэддля:
где
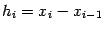
и
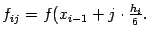
Таким образом, при применении формулы Уэддля на каждом очередном отрезке нужно вычислить 6 новых значений функции
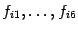
, а значение
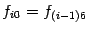
вычислять заново не нужно, оно было уже вычислено на предыдущем шаге.
Для ошибки формулы Уэддля 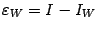 с постоянным шагом
с постоянным шагом 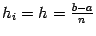 имеется такая оценка:
имеется такая оценка:
где
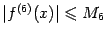
и
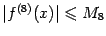
при всех
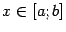
. При этом предполагается, что восьмая производная
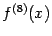
непрерывна на отрезке
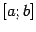
.
Таким образом, формула Уэддля является квадраткрной формулой шестого порядка точности. На практике формулы более высокого порядка точности, чем формула Уэддля, не используются. Формула " 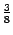 " используется редко. Если не устраивает формула Симпсона, то сразу переходят к формуле Уэддля.
" используется редко. Если не устраивает формула Симпсона, то сразу переходят к формуле Уэддля.
Замечание 5.2 Мы не затрагиваем здесь вопросов, связанных с
квадратурными формулами Гаусса (в которых, для повышения точности, точки
, в которых вычисляются значения функции

, выбираются специальным образом), а также другие вопросы приближённого нахождения интегралов, например, нахождение несобственных интегралов, осциллирующих интегралов и других интегралов специальных типов. Интересующихся этими вопросами мы отсылаем к книгам
Бахвалов Н. С., Жидков Н. П., Кобельков Г. М. Численные методы. -- М.: Наука, 1987,
Амосов А. А., Дубинский Ю. А., Копченова Н. В. Вычислительные методы для инженеров. -- М.: Высш. шк., 1994,
Рябенький В. С. Введение в вычислительную математику. -- М.: Наука, Физматлит, 1994.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
![]() многочленами степени 3, то получится формула, называемая кквадратурной формулой
многочленами степени 3, то получится формула, называемая кквадратурной формулой ![]() (три восьмых)":
(три восьмых)": 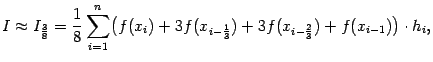
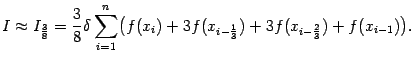
![]() и заменять интеграл ог
и заменять интеграл ог ![]() на каждом из отрезков
на каждом из отрезков ![]() на интеграл от
на интеграл от ![]() , то получится квадратурная формула, называемая формулой Уэддля:
, то получится квадратурная формула, называемая формулой Уэддля: 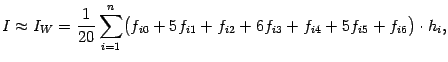
![]() с постоянным шагом
с постоянным шагом ![]() имеется такая оценка:
имеется такая оценка: 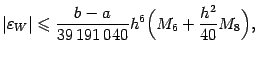
![]() " используется редко. Если не устраивает формула Симпсона, то сразу переходят к формуле Уэддля.
" используется редко. Если не устраивает формула Симпсона, то сразу переходят к формуле Уэддля.