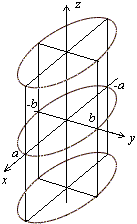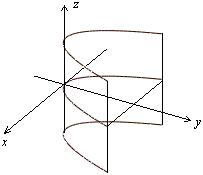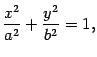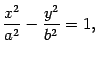‹-- Назад
Определение 13.9 Цилиндрической поверхностью называется геометрическое место параллельных прямых, пересекающих данную линию. Эта линия называется направляющей, а параллельные прямые -- образующими.
Рассмотрим уравнение вида
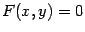 | (13.17) |
и покажем, что оно определяет цилиндрическую поверхность с образующими, параллельными оси
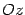
. Пусть
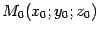
-- некоторая точка, координаты которой удовлетворяют уравнению (
13.17). Поскольку в это уравнение не входит явно переменная
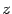
, ему будут удовлетворять координаты всех точек
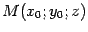
, где
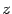
-- любое число. Следовательно, при любом
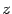
точка
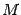
лежит на поверхности, определяемой уравнением (
13.17). Отсюда следует, что на поверхности целиком лежит прямая, проходящая через точку
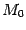
параллельно оси
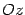
. А это означает, что поверхность, определяемая уравнением (
13.17), составлена из прямых, параллельных оси
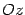
, то есть она является цилиндрической поверхностью.
Заметим, что на плоскости 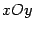 уравнение (13.17) определяет направляющую рассматриваемой цилиндрической поверхности.
уравнение (13.17) определяет направляющую рассматриваемой цилиндрической поверхности.
Итак, делаем вывод, что если уравнение поверхности не содержит в явном виде какой-либо переменной, то это уравнение определяет в пространстве цилиндрическую поверхность с образующими, параллельными оси отсутствующего переменного и направляющей, которая в плоскости двух других переменных имеет то же самое уравнение.
Нас будут интересовать только те цилиндрические поверхности, которые являются поверхностями второго порядка, а это значит, что уравнение (13.17), их задающее будет иметь вид (13.1).
Определение 13.10 Поверхность, которая в некоторой декартовой системе координат задается уравнением
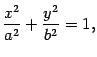 | (13.18) |
называется
эллиптическим цилиндром, поверхность, которая задается уравнением
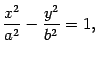 | (13.19) |
называется
гиперболическим цилиндром, а которая задается уравнением
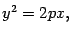 | (13.20) |
называется
параболическим цилиндром.
Для того чтобы построить поверхность, задаваемую уравнением (13.18), или уравнением (13.19), или (13.20), достаточно нарисовать на плоскости 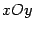 направляющую, уравнение которой на этой плоскости совпадает с уравнением самой поверхности, и затем через точки направляющей провести образующие параллельно оси
направляющую, уравнение которой на этой плоскости совпадает с уравнением самой поверхности, и затем через точки направляющей провести образующие параллельно оси 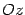 . Для наглядности следует построить также одно-два сечения плоскостями, параллельными плоскости
. Для наглядности следует построить также одно-два сечения плоскостями, параллельными плоскости 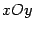 . В каждом таком сечении получим такую же кривую, как и исходная направляющая. Изображения этих цилиндров сечениями приведены на рисунках 13.27, 13.29 и 13.31, а их объемные изображения -- на рисунках 13.28, 13.30 и 13.32.
. В каждом таком сечении получим такую же кривую, как и исходная направляющая. Изображения этих цилиндров сечениями приведены на рисунках 13.27, 13.29 и 13.31, а их объемные изображения -- на рисунках 13.28, 13.30 и 13.32.
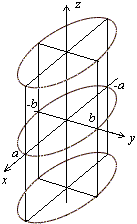
Рис.13.27.Изображение эллиптического цилиндра с помощью сечений
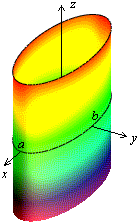
Рис.13.28.Эллиптический цилиндр
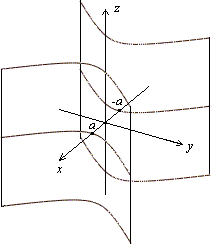
Рис.13.29.Изображение гипербоического цилиндра с помощью сечений
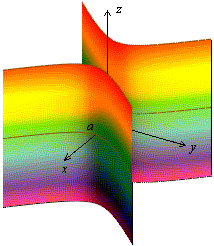
Рис.13.30.Гиперболический цилиндр
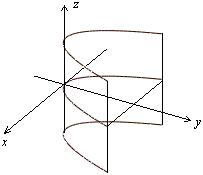
Рис.13.31.Изображение параболического цилиндра с помощью сечений
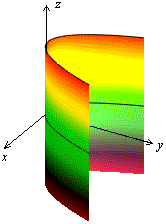
Рис.13.32.Параболический цилиндр
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
![]() уравнение (13.17) определяет направляющую рассматриваемой цилиндрической поверхности.
уравнение (13.17) определяет направляющую рассматриваемой цилиндрической поверхности. ![]() направляющую, уравнение которой на этой плоскости совпадает с уравнением самой поверхности, и затем через точки направляющей провести образующие параллельно оси
направляющую, уравнение которой на этой плоскости совпадает с уравнением самой поверхности, и затем через точки направляющей провести образующие параллельно оси ![]() . Для наглядности следует построить также одно-два сечения плоскостями, параллельными плоскости
. Для наглядности следует построить также одно-два сечения плоскостями, параллельными плоскости ![]() . В каждом таком сечении получим такую же кривую, как и исходная направляющая. Изображения этих цилиндров сечениями приведены на рисунках 13.27, 13.29 и 13.31, а их объемные изображения -- на рисунках 13.28, 13.30 и 13.32.
. В каждом таком сечении получим такую же кривую, как и исходная направляющая. Изображения этих цилиндров сечениями приведены на рисунках 13.27, 13.29 и 13.31, а их объемные изображения -- на рисунках 13.28, 13.30 и 13.32.