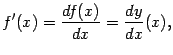‹-- Назад
Определение 4.3 Пусть дана функция

, и

-- внутренняя точка её области определения. Придадим аргументу приращение
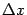
и рассмотрим приращение функции
Если это приращение
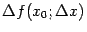
можно представить в виде
где величина
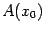
не зависит от приращения
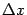
, а
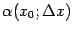
-- бесконечно малая при базе
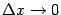
величина, имеющая больший порядок малости, чем
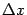
, то произведение
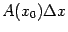
называется
дифференциалом функции  в точке
в точке 
и обозначается
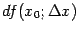
или просто
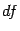
.
Таким образом, дифференциал 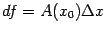 -- это функция двух аргументов
-- это функция двух аргументов  и
и 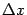 , причём от переменного приращения
, причём от переменного приращения 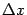 дифференциал зависит линейно (
дифференциал зависит линейно (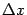 входит в выражение, задающее
входит в выражение, задающее 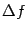 , как множитель, стоящий в первой степени). Заметим, что в формуле
, как множитель, стоящий в первой степени). Заметим, что в формуле
второе слагаемое в правой части имеет порядок малости, больший, чем у
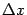
, и, следовательно, при
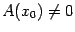
больший, чем у
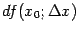
. Поэтому
дифференциал 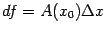 -- это главная, линейная по
-- это главная, линейная по 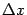 , часть приращения функции
, часть приращения функции.
Доказательство. Пусть функция  имеет дифференциал, то есть её приращение можно представить в виде
имеет дифференциал, то есть её приращение можно представить в виде 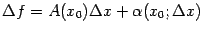 . Разделим обе части равенства на
. Разделим обе части равенства на 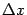 :
:
При
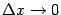
в правой части предел первого слагаемого равен
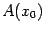
, поскольку эта величина не зависит от
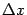
и, следовательно, при вычислении предела считается постоянной. Далее,
так как, по определению дифференциала,
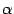
имеет более высокий порядок малости, нежели
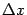
. Значит, существует предел
Но этот предел, по определению, равен производной
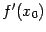
. Значит, функция имеет производную в точке

, и
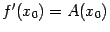
, откуда
Пусть теперь функция  имеет производную
имеет производную 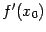 . Это означает, что
. Это означает, что 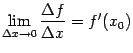 . По теореме о связи пределов и бесконечно малых, это эквивалентно тому, что величина
. По теореме о связи пределов и бесконечно малых, это эквивалентно тому, что величина 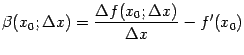 является бесконечно малой. Умножим обе части последнего равенства на
является бесконечно малой. Умножим обе части последнего равенства на 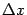 и получим:
и получим:
Получили представление приращения функции в виде
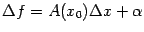
, где
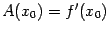
, а величина
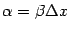
, очевидно, имеет больший порядок малости, чем
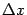
, поскольку
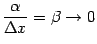
при
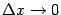
. Тем самым, функция

имеет в точке

дифференциал, который имеет вид
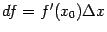
.
Геометрический смысл дифференциала 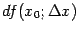 мы выясним, исходя из найденного ранее геометрического смысла производной. Поскольку производная
мы выясним, исходя из найденного ранее геометрического смысла производной. Поскольку производная 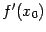 -- это угловой коэффициент
-- это угловой коэффициент 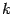 касательной к графику функции при
касательной к графику функции при 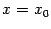 , то дифференциал
, то дифференциал 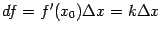 -- это приращение ординаты
-- это приращение ординаты 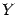 точки касательной
точки касательной
к графику функции
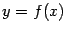
, когда абсцисса точки касательной получает приращение
:
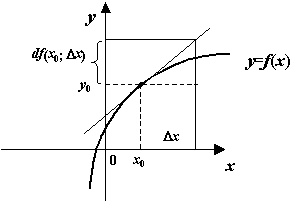
Рис.4.6.Дифференциал равен приращению ординаты касательной
Замечание 4.6 Заметим, что для функции

производная равна 1, так что дифференциал
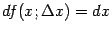
равен
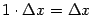
, то есть
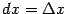
. Поэтому можно всюду вместо приращения независимой переменной
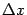
писать её дифференциал
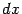
. При этом получается, что для произвольной дифференцируемой функции

Замечание 4.7 Часто в обозначении дифференциала функции пропускают второй аргумент
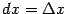
, от которого
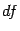
зависит линейно, и пишут короче:
Однако нужно чётко понимать, что это лищь сокращённая запись, и на самом деле дифференциал -- это функция двух аргументов

и
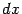
, линейная по
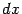
.
Замечание 4.8 Поскольку для функции
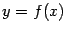
дифференциал записывается как
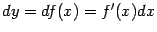
, то, деля на
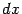
, получаем
что придаёт смысл обозначению производной в виде отношения дифференциалов. Это обозначение было введено нами ранее, однако выше мы не придавали дроби
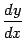
смысла некоторого отношения двух величин, а смогли сделать это только сейчас.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
![]() -- это функция двух аргументов
-- это функция двух аргументов ![]() и
и ![]() , причём от переменного приращения
, причём от переменного приращения ![]() дифференциал зависит линейно (
дифференциал зависит линейно (![]() входит в выражение, задающее
входит в выражение, задающее ![]() , как множитель, стоящий в первой степени). Заметим, что в формуле
, как множитель, стоящий в первой степени). Заметим, что в формуле ![]() имеет дифференциал, то есть её приращение можно представить в виде
имеет дифференциал, то есть её приращение можно представить в виде ![]() . Разделим обе части равенства на
. Разделим обе части равенства на ![]() :
: 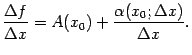
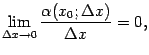
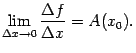
![]() имеет производную
имеет производную ![]() . Это означает, что
. Это означает, что 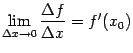 . По теореме о связи пределов и бесконечно малых, это эквивалентно тому, что величина
. По теореме о связи пределов и бесконечно малых, это эквивалентно тому, что величина 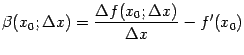 является бесконечно малой. Умножим обе части последнего равенства на
является бесконечно малой. Умножим обе части последнего равенства на ![]() и получим:
и получим: ![]() мы выясним, исходя из найденного ранее геометрического смысла производной. Поскольку производная
мы выясним, исходя из найденного ранее геометрического смысла производной. Поскольку производная ![]() -- это угловой коэффициент
-- это угловой коэффициент ![]() касательной к графику функции при
касательной к графику функции при ![]() , то дифференциал
, то дифференциал ![]() -- это приращение ординаты
-- это приращение ординаты ![]() точки касательной
точки касательной