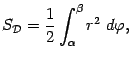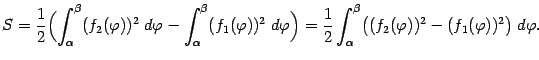‹-- Назад Напомним, что определением интеграла служит предел интегральных сумм, взятый при условии измельчения разбиения отрезка интегрирования. Этим определением мы воспользуемся для нахождения площади в следующем случае.
Пусть на плоскости фиксирована система полярных координат: полярными координатами точки 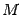 служат два числа
служат два числа 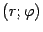 (
(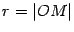 -- полярный радиус,
-- полярный радиус, 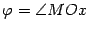 -- полярный угол).
-- полярный угол).
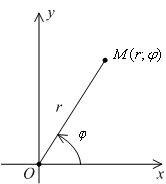
Рис.6.4.
Уравнение, задающее зависимость величины
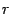
от полярного угла
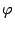
,
задаёт некоторую линию на плоскости. Будем предполагать, что функция
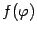
непрерывна при
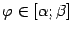
. Рассмотрим область
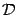
на плоскости, расположенную между выходящими из начала координат лучами
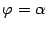
и
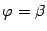
и линией
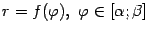
(эта область заштрихована на следующем чертеже).
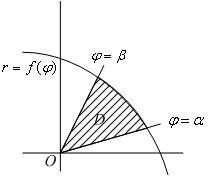
Рис.6.5.
Найдём площадь области
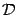
, вначале приблизив область ступенчатой фигурой следующего устройства. Область изменения угла
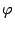
, то есть отрезок
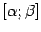
, разобьём на части точками деления
и выберем на каждом участке
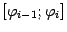
некоторую отмеченную точку
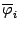
. Получаем размеченное разбиение

отрезка
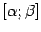
. Приближённо будем считать площадь
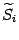
сектора области
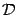
, лежащего между лучами
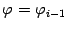
и
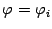
, равной площади
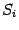
кругового сектора с тем же центральным углом
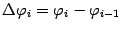
и радиусом, равным
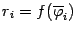
(см. рис.):
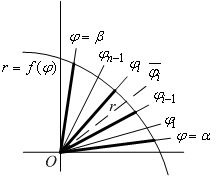
Рис.6.6.
Площадь кругового сектора подсчитывается по формуле
Значит, площадь всей области приближённо равна интегральной сумме
построенной по выбранному размеченному разбиению отрезка
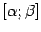
для функции
При неограниченном измельчении разбиения

, то есть при условии
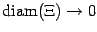
, эта интегральная сумма будет стремиться к площади области
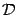
. С другой стороны, предел интегральных сумм для функции
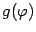
даст определённый интеграл от этой функции. Таким образом, получаем формулу площади:
Более кратко эту формулу можно записать так:
где имеется в виду, что вместо полярного радиуса
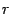
нужно подставить его выражение через полярный угол
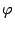
для зависимости, график которой ограничивает область снаружи.
Пример 6.3 Найдём площадь
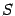
области, ограниченной частью спирали
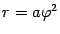
(
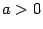
) при
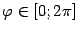
и отрезком
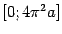
оси

(см. рис.).
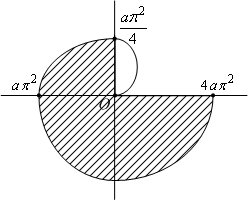
Рис.6.7.
Применяя формулу (
6.3), получаем:
Если область  имеет границу, состоящую из двух отрезков лучей
имеет границу, состоящую из двух отрезков лучей 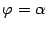 и
и 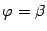 (эти отрезки могут вырождаться в одну точку) и двумя линиями, заданными уравнениями в полярных координатах:
(эти отрезки могут вырождаться в одну точку) и двумя линиями, заданными уравнениями в полярных координатах: 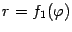 и
и 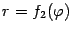 , причём
, причём 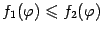 при всех
при всех 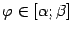 (см. рис.), то площадь
(см. рис.), то площадь 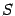 области
области 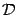 можно представить как разность двух площадей:
можно представить как разность двух площадей: 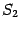 -- площади области, лежащей между лучами
-- площади области, лежащей между лучами 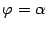 ,
, 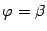 и линией
и линией 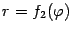 , -- и
, -- и 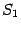 -- площади области, лежащей между лучами
-- площади области, лежащей между лучами 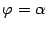 ,
, 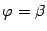 и линией
и линией 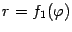 .
.
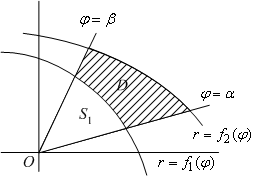
Рис.6.8.
Каждую из площадей
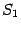
и
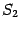
можно подсчитать по формуле (
6.3), так что получаем в итоге
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
![]() служат два числа
служат два числа ![]() (
(![]() -- полярный радиус,
-- полярный радиус, ![]() -- полярный угол).
-- полярный угол). 


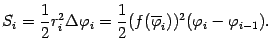
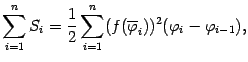
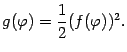
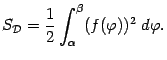

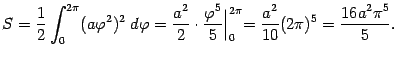
![]() имеет границу, состоящую из двух отрезков лучей
имеет границу, состоящую из двух отрезков лучей ![]() и
и ![]() (эти отрезки могут вырождаться в одну точку) и двумя линиями, заданными уравнениями в полярных координатах:
(эти отрезки могут вырождаться в одну точку) и двумя линиями, заданными уравнениями в полярных координатах: ![]() и
и ![]() , причём
, причём ![]() при всех
при всех ![]() (см. рис.), то площадь
(см. рис.), то площадь ![]() области
области ![]() можно представить как разность двух площадей:
можно представить как разность двух площадей: ![]() -- площади области, лежащей между лучами
-- площади области, лежащей между лучами ![]() ,
, ![]() и линией
и линией ![]() , -- и
, -- и ![]() -- площади области, лежащей между лучами
-- площади области, лежащей между лучами ![]() ,
, ![]() и линией
и линией ![]() .
.