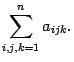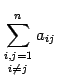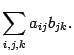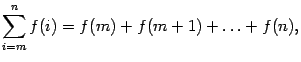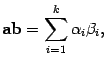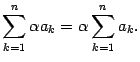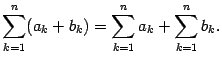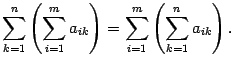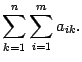‹-- Назад В математике для записи сумм, содержащих много слагаемых, или в случае, когда число слагаемых обозначено буквой, применяется следующая запись:
которая расшифровывается так
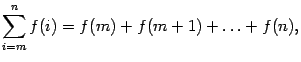 | (14.1) |
где
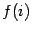
-- функция целочисленного аргумента. Здесь символ
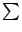
(большая греческая буква "сигма") означает суммирование. Запись
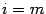
внизу символа суммирования показывает, что переменная, которая меняет свои значения от слагаемого к слагаемому, обозначена буквой
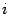
и что начальное значение этой переменной равно
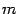
. Запись вверху обозначает последнее значение, которое принимает переменная
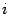
.
Пример 14.2 Вычислим несколько сумм:
1) 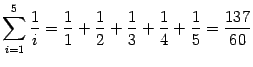 .
.
2) 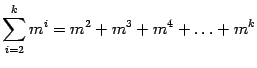 . Так как в правой части стоит сумма геометрической прогрессии с первым членом равным
. Так как в правой части стоит сумма геометрической прогрессии с первым членом равным 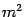 и знаменателем прогрессии равным
и знаменателем прогрессии равным 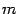 , то эту сумму легко найти
, то эту сумму легко найти
3) 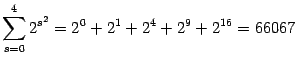 .
.
4) 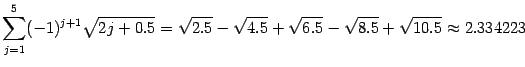 .
.
5) 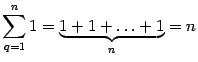 .
.
В курсе линейной алгебры чаще всего будут встречаться суммы вида 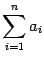 . Здесь переменная с индексом рассматривается как функция от своего индекса. Поэтому
. Здесь переменная с индексом рассматривается как функция от своего индекса. Поэтому
С помощью знака суммы формулу (
10.1) скалярного произведения векторов можно записать так:
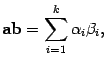 | (14.2) |
где для трехмерного пространства
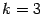
, для плоскости
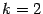
.
Для единообразия будем считать, что
и говорить, что это сумма, содержащая одно слагаемое.
Замечание 14.1 Буква, стоящая внизу под знаком суммы (индекс суммирования),
не влияет на результат суммирования. Важно лишь, как от этого индекса зависит суммируемая величина. Например,
Или
в правой части никакой буквы
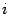
нет, значит, и результат от
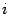
не зависит.
Предложение 14.1 Множитель, не зависящий от индекса суммирования, может быть вынесен за знак суммы:
Доказательство этого предложения предоставляется читателю.
Предложение 14.2 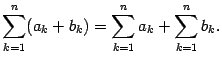 | (14.3) |
Это предложение является частным случаем следующего утверждения.
Доказательство. Пусть
Тогда
Раскроем скобки в правой части этого равенства. Получим сумму элементов
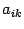
при всех допустимых значениях индексов суммирования. Слагаемые сгруппируем по-другому, а именно, сначала соберем все слагаемые, у которых первый индекс равен 1, потом, у которых первый индекс равен 2 и т.д. Получим
Заменив в этом равенстве
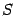
в левой части его выражением через знаки суммирования, получим формулу (
14.4).
Замечание 14.2 Двойные суммы из равенства (
14.4) можно записывать и без использования скобок
Нужно помнить, что двойная сумма означает сумму элементов 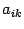 для всех допустимых значений индексов суммирования. По этой же причине, если встречается запись, содержащая подряд три или более символов суммирования, то порядок расстановки этих символов можно менять произвольно.
для всех допустимых значений индексов суммирования. По этой же причине, если встречается запись, содержащая подряд три или более символов суммирования, то порядок расстановки этих символов можно менять произвольно.
Если границы изменения всех индексов суммирования одинаковы, то можно для суммирования по нескольким индексам использовать запись вида
Иногда под символом суммы указывают дополнительные условия, налагаемые на индексы суммирования. Так запись
означает, что в сумму не включаются величины
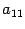
,
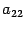
,...,
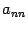
, то есть
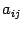
с равными индексами.
Иногда в записи суммы не указываются границы изменения индексов, например,
Такая запись используется, когда значения, которые могут принимать индексы, очевидны из предыдущего текста или будут оговорены сразу после окончания формулы.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
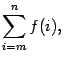
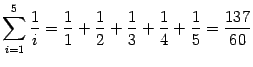 .
. 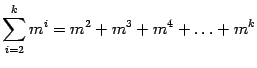 . Так как в правой части стоит сумма геометрической прогрессии с первым членом равным
. Так как в правой части стоит сумма геометрической прогрессии с первым членом равным ![]() и знаменателем прогрессии равным
и знаменателем прогрессии равным ![]() , то эту сумму легко найти
, то эту сумму легко найти 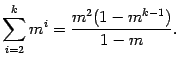
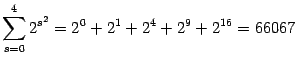 .
. 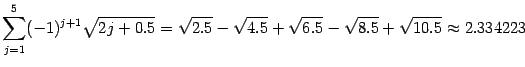 .
. 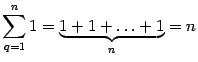 .
. ![]() . Здесь переменная с индексом рассматривается как функция от своего индекса. Поэтому
. Здесь переменная с индексом рассматривается как функция от своего индекса. Поэтому 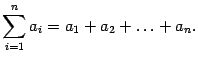
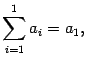
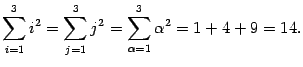
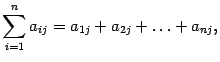
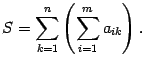
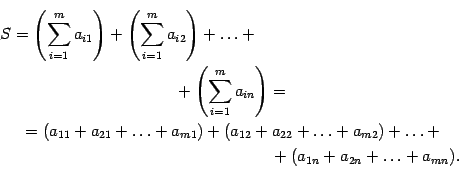
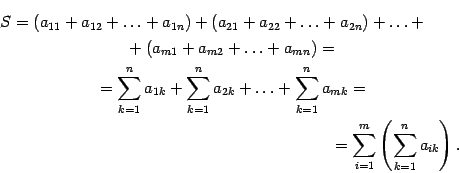
![]() для всех допустимых значений индексов суммирования. По этой же причине, если встречается запись, содержащая подряд три или более символов суммирования, то порядок расстановки этих символов можно менять произвольно.
для всех допустимых значений индексов суммирования. По этой же причине, если встречается запись, содержащая подряд три или более символов суммирования, то порядок расстановки этих символов можно менять произвольно.