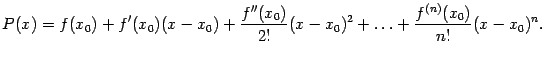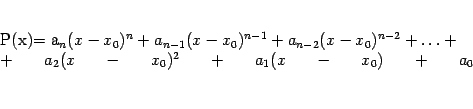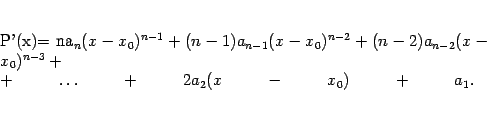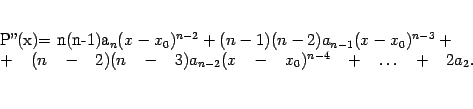‹-- Назад
Многочлен Тейлора
Многочлен ![]() , наиболее подходящий (с некоторой точки зрения) для этой цели, называется многочленом Тейлора для данной функции; найдя его по заданной функции
, наиболее подходящий (с некоторой точки зрения) для этой цели, называется многочленом Тейлора для данной функции; найдя его по заданной функции ![]() , мы сможем вместо сложного вычисления значений функции
, мы сможем вместо сложного вычисления значений функции ![]() приближённо заменять это вычисление на вычисление значений многочлена16
приближённо заменять это вычисление на вычисление значений многочлена16 ![]() .
.
Уточним теперь постановку задачи. Пусть функция ![]() определена в некоторой окрестности
определена в некоторой окрестности ![]() некоторой точки
некоторой точки ![]() и имеет всюду в окрестности
и имеет всюду в окрестности ![]() производные
производные ![]() при
при ![]() . Многочленом Тейлора степени
. Многочленом Тейлора степени ![]() в точке
в точке ![]() называется такой многочлен
называется такой многочлен ![]() степени
степени ![]() , такой, что его значение и значение всех его производных, вычисленные в точке
, такой, что его значение и значение всех его производных, вычисленные в точке ![]() , равны соответствующим значениям функции
, равны соответствующим значениям функции ![]() и её производных
и её производных ![]() до порядка
до порядка ![]() в этой же точке:
в этой же точке:
Если это условие совпадения выполнено, то графики функций ![]() и
и ![]() , по крайней мере при
, по крайней мере при ![]() , близких к
, близких к ![]() , будут идти весьма тесно друг к другу. Равенство
, будут идти весьма тесно друг к другу. Равенство
Для нахождения вида многочлена Тейлора для заданной функции сделаем сначала следующее замечание. Любой многочлен ![]() степени
степени ![]() вида
вида
Действительно, положив ![]() , мы можем подставить
, мы можем подставить ![]() в правую часть формулы
в правую часть формулы ![]() , раскрыть степени
, раскрыть степени ![]() при
при ![]() по формуле бинома Ньютона, а потом привести подобные члены. Все коэффициенты
по формуле бинома Ньютона, а потом привести подобные члены. Все коэффициенты ![]() (кроме
(кроме ![]() ) и свободный член при этом изменятся на некоторые другие (
) и свободный член при этом изменятся на некоторые другие (![]() в нашей формуле), но получится многочлен по степеням бинома
в нашей формуле), но получится многочлен по степеням бинома ![]() , имеющий ту же степень
, имеющий ту же степень ![]() .
.
Итак, будем предполагать, что многочлен Тейлора мы ищем в виде
при некоторых коэффициентах
Учтём требование к значению многочлена: ![]() . Подставив в равенство (Тейлор 1)
. Подставив в равенство (Тейлор 1) ![]() , получим, что
, получим, что ![]() , так как все остальные слагаемые обратятся в 0. Тем самым
, так как все остальные слагаемые обратятся в 0. Тем самым
Учтём затем требование к значению первой производной многочлена: ![]() . Производная от
. Производная от ![]() равна
равна
Подставив в равенство (Тейлор 2) значение
Следующее требование -- к значению второй производной многочлена: ![]() . Вторая производная от
. Вторая производная от ![]() равна
равна
Снова подставив в равенство (Тейлор 3) значение
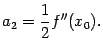
Далее нетрудно сообразить, что получится ![]() , откуда
, откуда
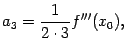
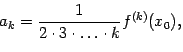 |
при
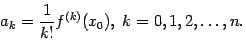 |
Итак, мы получили, что многочлен Тейлора для функции ![]() в точке
в точке ![]() имеет вид
имеет вид