‹-- Назад Рассмотрим несколько важнейших элементарных функций и найдём для них многочлены Тейлора при 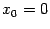 .
.
1. Рассмотрим функцию 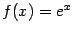 . Все её производные совпадают с ней:
. Все её производные совпадают с ней: 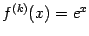 , так что коэффициенты Тейлора в точке
, так что коэффициенты Тейлора в точке 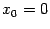 равны
равны
Поэтому формула Тейлора для экспоненты такова:
2. Рассмотрим функцию 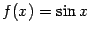 . Её производные чередуются в таком порядке:
. Её производные чередуются в таком порядке:
а затем цикл повторяется. Поэтому при подстановке
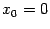
также возникает повторение:
и т. д. Все производные с чётными номерами оказываются равными 0; производные с нечётными номерами
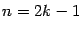
равны 1 при
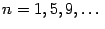
, то есть при
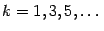
, и
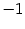
при
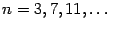
, то есть при
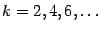
. Таким образом,
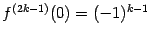
при всех
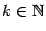
и коэффициенты Тейлора равны
Получаем формулу Тейлора для синуса:
Заметим, что мы можем записать остаточный член
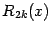
вместо
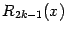
(как можно было бы подумать), поскольку можно считать, что слагаемое порядка
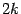
, с коэффициентом, равным 0, тоже включено в многочлен Тейлора.
3. Для функции 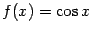 производные также чередуются с циклом длины 4, как и для синуса. Значения в точке
производные также чередуются с циклом длины 4, как и для синуса. Значения в точке 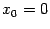 имеют то же чередование:
имеют то же чередование:
Нетрудно видеть, что
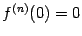
при
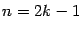
,
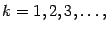
и
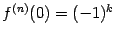
при
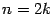
,
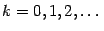
. Поэтому разложение косинуса по формуле Тейлора имеет вид
Здесь мы также считаем, что последним в многочлене Тейлора выписано слагаемое, содержащее
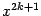
с нулевым коэффициентом.
Упражнение 6.1 Найдите формулу для производной произвольного порядка от функции
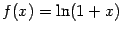
. Вычислите значения этих производных при
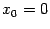
и коэффициенты Тейлора. Покажите, что имеет место разложение
Упражнение 6.2 Найдите формулу для производной произвольного порядка от функции
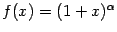
при фиксированном
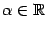
. Вычислите значения этих производных при
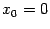
и коэффициенты Тейлора. Покажите, что имеет место разложение
Упражнение 6.3 Покажите, что разложения по формуле Тейлора для функций
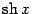
и
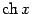
выглядят так:
и
Сравните найденные разложения с разложениями для
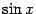
,
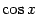
и
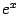
.
На основе полученных разложений можно получать и разложения многих других функций.
Пример 6.1 Рассмотрим функцию
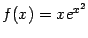
. Найдём её разложение по формуле Тейлора в точке
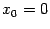
. Начнём с того, что напишем ранее найденное разложение для экспоненты,
и положим в нём
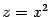
:
Теперь умножим левую и правую части этой формулы на
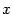
:
Заметим, что бесконечно малое при
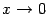
выражение
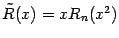
имеет тот же или больший порядок малости, как
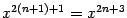
, и поэтому может рассматриваться как остаточный член
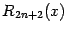
в формуле Тейлора для

, а предыдущие слагаемые в правой части формулы -- как многочлен Тейлора данной функции. Так что её искомое разложение найдено.
Разберём теперь пример того, как полученные разложения элементарных функций можно использовать для раскрытия некоторых неопределённостей.
Пример 6.2 Найдём предел
Для начала найдём разложение по формуле Тейлора в точке 0 для числителя:
где через
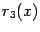
обозначен остаточный член, имеющий тот же порядок малости, что и
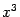
. Разложение для знаменателя имеет вид:
где остаточные члены
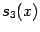
и
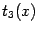
тоже имеют тот же порядок малости, что и
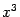
, при
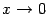
. Выполняя приведение подобных членов, получаем, что знаменатель равен
Итак,
Заметим, что этот способ раскрытия неопределённостей типа  в некоторых случаях, подобных разобранному в примере, менее трудоёмок, чем применение правила Лопиталя.
в некоторых случаях, подобных разобранному в примере, менее трудоёмок, чем применение правила Лопиталя.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
![]() .
. ![]() . Все её производные совпадают с ней:
. Все её производные совпадают с ней: ![]() , так что коэффициенты Тейлора в точке
, так что коэффициенты Тейлора в точке ![]() равны
равны 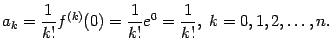
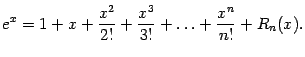
![]() . Её производные чередуются в таком порядке:
. Её производные чередуются в таком порядке: 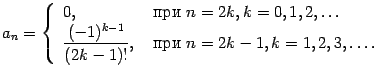
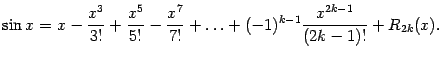
![]() производные также чередуются с циклом длины 4, как и для синуса. Значения в точке
производные также чередуются с циклом длины 4, как и для синуса. Значения в точке ![]() имеют то же чередование:
имеют то же чередование: 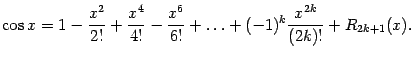
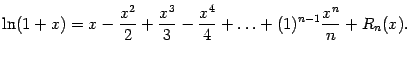
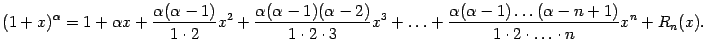
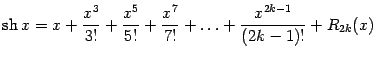
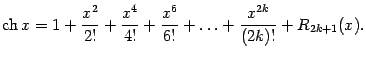
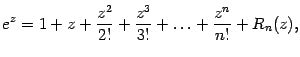
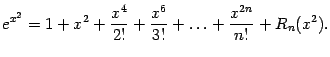
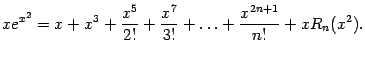
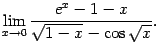
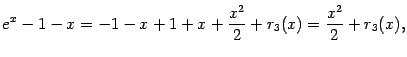
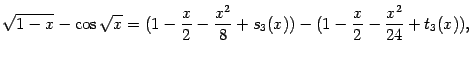
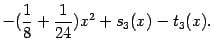
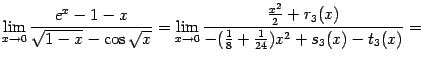
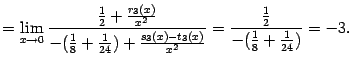
![]() в некоторых случаях, подобных разобранному в примере, менее трудоёмок, чем применение правила Лопиталя.
в некоторых случаях, подобных разобранному в примере, менее трудоёмок, чем применение правила Лопиталя.