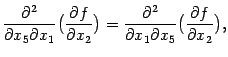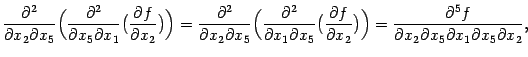‹-- Назад Ранее мы отмечали, что при некоторых дополнительных предположениях частные производные высших порядков, отличающиеся лишь порядком дифференцирований, совпадают. Теперь мы уточним эти предположения и сформулируем утверждение о равенстве смешанных производных. Оказывается, достаточно предположить непрерывность этих смешанных производных.
Доказательство. Пусть 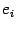 и
и 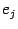 -- единичные базисные векторы в
-- единичные базисные векторы в 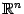 вида
вида 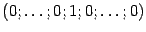 , где 1 стоит, соответственно, на
, где 1 стоит, соответственно, на 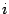 -м и
-м и 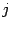 -м местах. Пусть
-м местах. Пусть 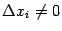 и
и 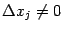 (для определённости будем далее считать, что
(для определённости будем далее считать, что 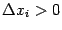 и
и 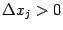 ). Рассмотрим приращения
). Рассмотрим приращения
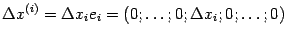
и
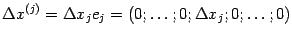
и будем считать, что числа
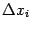
и
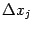
достаточно малы, так что точка
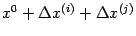
лежит в окрестности
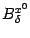
.
Положим
и введём две функции:
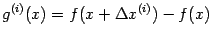
и
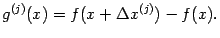
Тогда
и
Полученные разности
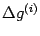
и
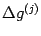
тождественно равны друг другу. Применим к первой из них теорему Лагранжа на отрезке
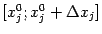
по переменной
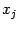
:
где
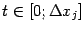
-- некоторая промежуточная точка. Аналогично, применяя ко второй из разностей,
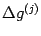
, теорему Лагранжа на отрезке
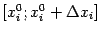
по переменной
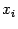
, получаем
где
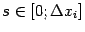
-- некоторая промежуточная точка. (Попутный вопрос к читателю: почему к функциям
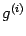
и
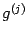
можно было применять теорему Лагранжа, и почему получились именно такие выражения, как написано выше?)
К получившимся в правых частях разностям частных производных
и
снова применим теорему Лагранжа и получим
где
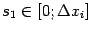
, и
где
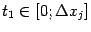
, и, следовательно,
(Снова продумайте вопрос о том, почему можно было применять теорему Лагранжа.) Так как по предположению
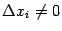
и
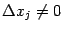
, то на
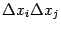
можно левую и правую части поделить и получить
При
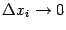
и
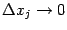
величины
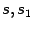
и
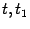
стремятся к 0. Поэтому, переходя к пределу при
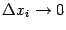
и
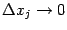
в обеих частях последнего равенства, получаем
в силу того, что, по предположению теоремы, обе смешанные частные производные непрерывны в точке
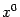
. Итак, теорема доказана.
Из доказанной теоремы вытекает такое следствие:
Доказательство. Для доказательства этого следствия воспользуемся методом "пузырьковой сортировки": будем переставлять, пользуясь доказанной теоремой и проверяя списки номеров переменных слева направо, те соседние дифференцирования в производных 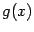 и
и 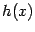 , в которых
, в которых 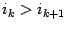 или
или 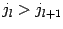 .
.
В результате конечного числа таких перестановок, оба значения 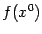 и
и 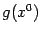 окажутся равными значению одной и той же смешанной частной производной
окажутся равными значению одной и той же смешанной частной производной
в которой номера переменных идут в порядке неубывания, то есть
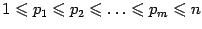
. Следовательно, совпадают числа
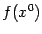
и
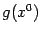
, что и требовалось доказать.
Замечание 7.4 Приводя смешанную частную производную к виду
где
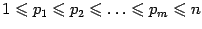
, мы можем записать её в виде
где
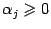
и
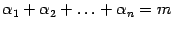
. (Если
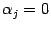
, то соответствующий "множитель" в "знаменателек мы не пишем, а вместо
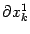
пишем просто
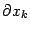
.)
Пример 7.17 Если две производных
и
непрерывны, то они совпадают, так как соответствующие списки номеров переменных равны, соответственно,
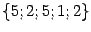
и
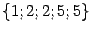
и отличаются лишь порядком перечисления номеров. Значит, частные производные отличаются лишь порядком дифференцирований, и поэтому
В этом примере перестановки дифференцирований можно выполнить в следующем порядке:
При первой и четвёртой перестановках переставляемые диффиеренцирования -- внешние и выполняются непосредственным применением теоремы к функциям
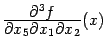
и
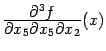
соответственно; эти производные третьего порядка предполагаются непрерывными. При остальных перестановках переставляются внутренние дифференцирования. При этом, например, при второй перестановке, рассуждаем так: имеем равенство
Функции
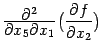
и
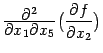
непрерывны по предположению, так как содержат меньше дифференцирований по
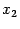
и
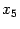
, чем исходные производные пятого порядка, и столько же дифференцирований по остальным переменным. Поэтому
и мы можем продолжить равенство:
и вторая перестановка обоснована.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
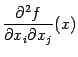 и
и 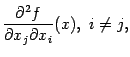
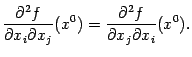
![]() и
и ![]() -- единичные базисные векторы в
-- единичные базисные векторы в ![]() вида
вида ![]() , где 1 стоит, соответственно, на
, где 1 стоит, соответственно, на ![]() -м и
-м и ![]() -м местах. Пусть
-м местах. Пусть ![]() и
и ![]() (для определённости будем далее считать, что
(для определённости будем далее считать, что ![]() и
и ![]() ). Рассмотрим приращения
). Рассмотрим приращения 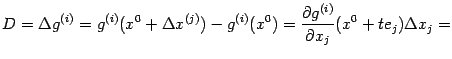
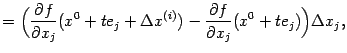
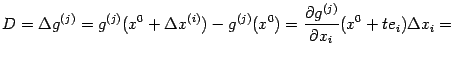
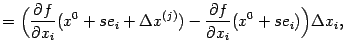
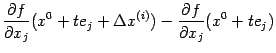
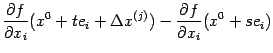
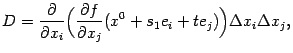
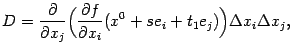
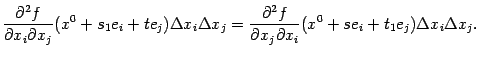
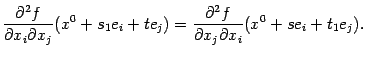
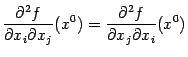
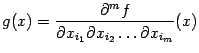
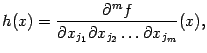
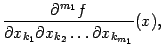
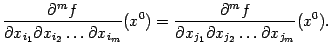
![]() и
и ![]() , в которых
, в которых ![]() или
или ![]() .
. ![]() и
и ![]() окажутся равными значению одной и той же смешанной частной производной
окажутся равными значению одной и той же смешанной частной производной 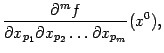
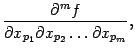
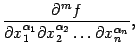
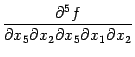
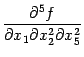
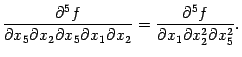
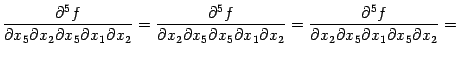
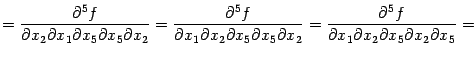
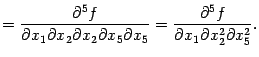
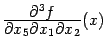 и
и 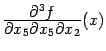 соответственно; эти производные третьего порядка предполагаются непрерывными. При остальных перестановках переставляются внутренние дифференцирования. При этом, например, при второй перестановке, рассуждаем так: имеем равенство
соответственно; эти производные третьего порядка предполагаются непрерывными. При остальных перестановках переставляются внутренние дифференцирования. При этом, например, при второй перестановке, рассуждаем так: имеем равенство 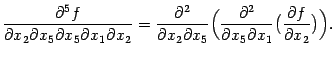
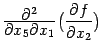 и
и 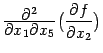 непрерывны по предположению, так как содержат меньше дифференцирований по
непрерывны по предположению, так как содержат меньше дифференцирований по