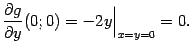‹-- Назад
Теорема о неявной функции
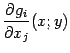 и
и 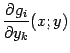 (
( Рассмотрим квадратную матрицу из частных производных функций ![]() по переменным
по переменным ![]() , вычисленным в точке
, вычисленным в точке ![]() :
:
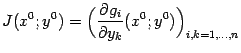
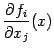 в шаре
в шаре
Рассмотренная квадратная матрица ![]() , составленная из производных функций
, составленная из производных функций ![]() по переменным
по переменным ![]() , называется матрицей Якоби вектор-функции
, называется матрицей Якоби вектор-функции ![]() по переменным
по переменным ![]() и часто обозначается
и часто обозначается 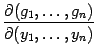 или просто
или просто ![]() . Её определитель
. Её определитель ![]() называется якобианом вектор-функции
называется якобианом вектор-функции ![]() по переменным
по переменным ![]() .
.
Утверждение теоремы означает, что векторное равенство ![]() задаёт, при выполнении предположения теоремы, некоторую вектор-функцию
задаёт, при выполнении предположения теоремы, некоторую вектор-функцию ![]() , такую что
, такую что ![]() , то есть из условия
, то есть из условия ![]() можно выразить
можно выразить ![]() через
через ![]() , если якобиан от
, если якобиан от ![]() по
по ![]() не равен 0. При этом говорят, что уравнение
не равен 0. При этом говорят, что уравнение ![]() неявно задаёт функцию
неявно задаёт функцию ![]() .
.
Доказательство сформулированной теоремы, ввиду его значительного объёма, мы не приводим здесь. Читатель может найти его в учебнике
Никольский С. М. Курс математического анализа, т. 1. -- М.: Наука, 1991. -- С. 304 - 308.
Отметим, что эта теорема содержательна и нетривиальна уже при ![]() и
и ![]() . Тогда её можно сформулировать так:
. Тогда её можно сформулировать так:
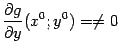 , то существует такая функция
, то существует такая функция 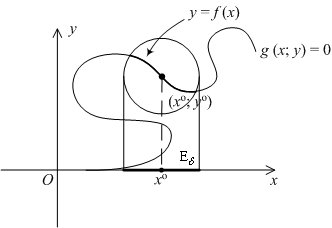
Отметим также, что важнейшим условием в теореме является требование невырожденности матрицы Якоби; в одномерном случае (то есть при
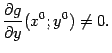
Однако условие теоремы о неявной функции для такой функции ![]() не выполнено:
не выполнено:
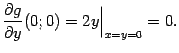
Вот ещё один пример, в котором, напротив, множество ![]() "слишком велико", чтобы быть графиком:
"слишком велико", чтобы быть графиком:
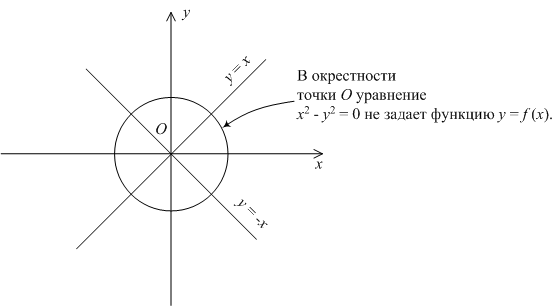
В окрестности начала координат это множество не является графиком никакой функции, поскольку каждому