‹-- Назад
Экстремум функции и необходимое условие экстремума
Напомним определение локального экстремума функции.
Понятия локальный максимум и локальный минимум объединяются термином локальный экстремум.
Следующая теорема даёт необходимое условие того, чтобы точка ![]() была точкой локального экстремума функции
была точкой локального экстремума функции ![]() .
.
Доказательство этой теоремы сразу же следует из теоремы Ферма (см. гл. 5).
Утверждение теоремы можно переформулировать так:
если функция ![]() имеет локальный экстремум в точке
имеет локальный экстремум в точке ![]() , то либо
, то либо
1) ![]() , либо
, либо
2) производная ![]() не существует.
не существует.
Точка ![]() называется критической точкой функции
называется критической точкой функции ![]() , если
, если ![]() непрерывна в этой точке и либо
непрерывна в этой точке и либо ![]() , либо
, либо ![]() не существует. В первом случае (то есть при
не существует. В первом случае (то есть при ![]() ) точка
) точка ![]() называется также стационарной точкой функции
называется также стационарной точкой функции ![]() .
.
Итак, локальный экстремум функции ![]() может наблюдаться лишь в одной из критических точек этой функции.
может наблюдаться лишь в одной из критических точек этой функции.
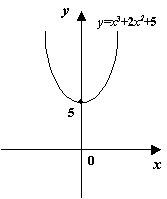
Записав функцию в виде ![]() , легко увидеть, что в точках
, легко увидеть, что в точках ![]() функция имеет минимум, так как в этих точках выражение
функция имеет минимум, так как в этих точках выражение ![]() обращается в 0, и
обращается в 0, и
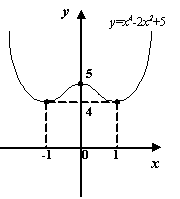
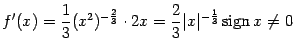
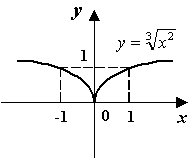
Не следует думать, что любая критическая точка функции даёт либо локальный максимум, либо локальный минимум. В некоторых критических точках экстремума может не оказаться вовсе.
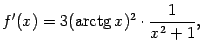
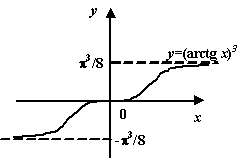
Пусть требуется отыскать максимальное и минимальное значения функции ![]() , непрерывной на замкнутом отрезке
, непрерывной на замкнутом отрезке ![]() . Согласно сказанному выше, если точка экстремума (максимума либо минимума) -- это внутренняя точка отрезка, то эта точка обязана быть критической. Следовательно, точка экстремума
. Согласно сказанному выше, если точка экстремума (максимума либо минимума) -- это внутренняя точка отрезка, то эта точка обязана быть критической. Следовательно, точка экстремума ![]() на
на ![]() -- это либо критическая точка, либо один из концов отрезка.
-- это либо критическая точка, либо один из концов отрезка.
Отсюда следует такой способ поиска максимума и минимума функции на ![]() : надо найти список "подозрительных" точек, включив в него: а) концы отрезка, то есть точки
: надо найти список "подозрительных" точек, включив в него: а) концы отрезка, то есть точки ![]() и
и ![]() ; б) стационарные точки, то есть все решения уравнения
; б) стационарные точки, то есть все решения уравнения ![]() ; в) критические точки, не являющиеся стационарными, то есть те точки отрезка, в которых функция непрерывна, но производная
; в) критические точки, не являющиеся стационарными, то есть те точки отрезка, в которых функция непрерывна, но производная ![]() не существует. Как правило, в этот список "подозрительных" точек входит конечное число точек. Во всех этих точках можно вычислить значение функции; максимальное и минимальное значение функции на отрезке будут содержаться в этом наборе значений, и их можно будет легко отыскать, а заодно установить и те значения
не существует. Как правило, в этот список "подозрительных" точек входит конечное число точек. Во всех этих точках можно вычислить значение функции; максимальное и минимальное значение функции на отрезке будут содержаться в этом наборе значений, и их можно будет легко отыскать, а заодно установить и те значения ![]() , при которых эти экстремальные значения достигаются.
, при которых эти экстремальные значения достигаются.
Имеем: ![]() . Производная существует при всех
. Производная существует при всех ![]() , так что все критические точки функции являются стационарными, а стационарные точки задаются уравнением
, так что все критические точки функции являются стационарными, а стационарные точки задаются уравнением ![]() . Это квадратное уравнение имеет корни
. Это квадратное уравнение имеет корни ![]() и
и ![]() ; первый корень не попадает на расматриваемый отрезок
; первый корень не попадает на расматриваемый отрезок ![]() , а второй попадает. Поэтому список "подозрительных" точек таков:
, а второй попадает. Поэтому список "подозрительных" точек таков: ![]() (оба конца отрезка и стационарная точка).
(оба конца отрезка и стационарная точка).
Вычисляем значения функции во всех точках списка: