‹-- Назад
Определение 8.1 Пусть кривая
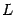
задана как график функции
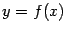
и
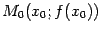
-- некоторая точка этой кривой. Будем предполагать, что функция

дифференцируема в некоторой окрестности точки

, так что при

из этой окрестности к графику
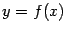
можно проводить касательные, составляющие угол
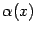
с осью
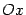
.
Кривизной кривой 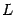 в точке
в точке 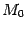 (или при
(или при 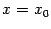 ) называется число
) называется число
где
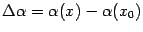
-- угол поворота касательной при переходе точки касания из
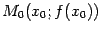
в
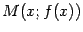
и
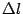
-- длина части линии
21 
между точками
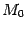
и
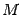
.
Смысл предела, определяющего кривизну, -- это скорость поворота касательной в точке 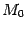 , в расчёте на единицу длины дуги.
, в расчёте на единицу длины дуги.
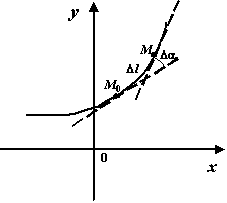
Рис.8.1.Поворот касательной при переходе из точки 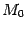 в точку
в точку 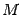
Доказательство. Пусть 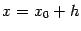 -- точка, близкая к
-- точка, близкая к  (будем считать для наглядности, что
(будем считать для наглядности, что 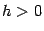 ). По геометрическому смыслу производной,
). По геометрическому смыслу производной, 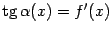 , откуда
, откуда 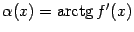 . При малых
. При малых 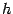 дуга
дуга 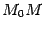 весьма близка к хорде
весьма близка к хорде 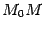 , и интуитивно ясно, что для гладкой кривой
, и интуитивно ясно, что для гладкой кривой 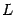 предел отношения длины дуги
предел отношения длины дуги 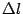 к длине хорды
к длине хорды 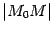 равен 1, то есть эти две бесконечно малых при
равен 1, то есть эти две бесконечно малых при 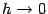 величины эквивалентны22. Хорда имеет длину
величины эквивалентны22. Хорда имеет длину 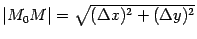 , где
, где 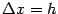 и
и 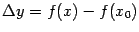 -- приращения координат при переходе от точки
-- приращения координат при переходе от точки 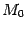 к точке
к точке 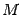 . Рассмотрим предел
. Рассмотрим предел 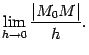 Имеем, очевидно,
Имеем, очевидно,
откуда
Поскольку
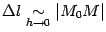
, то, заменив числитель на эквивалентную бесконечно малую, получаем, что
Теперь преобразуем отношение
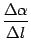
к виду
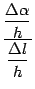
. Имеем тогда
Осталось вычислить производную, стоящую в числителе:
Это приводит нас к доказываемой формуле
Пример 8.1 Найдём кривизну параболы
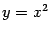
при произвольном значении

. Поскольку
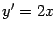
и
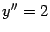
, имеем
Заметим, что кривизна параболы убывает при росте 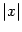 и принимает максимальное значение 2 при
и принимает максимальное значение 2 при  , то есть в вершине параболы.
, то есть в вершине параболы.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
![]() в точке
в точке ![]() (или при
(или при ![]() ) называется число
) называется число 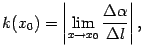
![]() , в расчёте на единицу длины дуги.
, в расчёте на единицу длины дуги. 
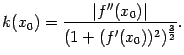
![]() -- точка, близкая к
-- точка, близкая к ![]() (будем считать для наглядности, что
(будем считать для наглядности, что ![]() ). По геометрическому смыслу производной,
). По геометрическому смыслу производной, ![]() , откуда
, откуда ![]() . При малых
. При малых ![]() дуга
дуга ![]() весьма близка к хорде
весьма близка к хорде ![]() , и интуитивно ясно, что для гладкой кривой
, и интуитивно ясно, что для гладкой кривой ![]() предел отношения длины дуги
предел отношения длины дуги ![]() к длине хорды
к длине хорды ![]() равен 1, то есть эти две бесконечно малых при
равен 1, то есть эти две бесконечно малых при ![]() величины эквивалентны22. Хорда имеет длину
величины эквивалентны22. Хорда имеет длину ![]() , где
, где ![]() и
и ![]() -- приращения координат при переходе от точки
-- приращения координат при переходе от точки ![]() к точке
к точке ![]() . Рассмотрим предел
. Рассмотрим предел 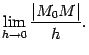 Имеем, очевидно,
Имеем, очевидно, 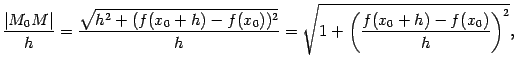
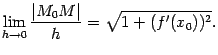
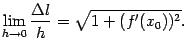
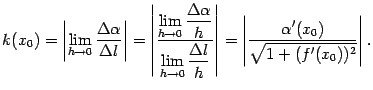
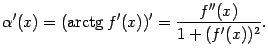
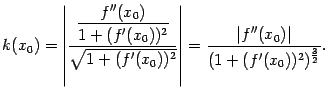
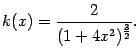
![]() и принимает максимальное значение 2 при
и принимает максимальное значение 2 при ![]() , то есть в вершине параболы.
, то есть в вершине параболы.