‹-- Назад Рассмотрим линейное пространство

и преобразование

этого пространства, то есть закон, по которому каждому вектору
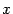
из

соответствует вектор
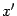
из того же пространства. Вектор
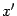
называется
образом вектора 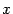
и обозначается
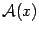
, а вектор
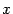
называется
прообразом вектора 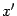
.
Определение 19.1 Преобразование

линейного пространства

называется
линейным, если для любых векторов
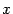
и
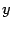
и любого числа
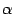
выполнены равенства
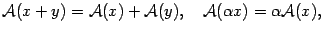 | (19.1) |
то есть образ суммы векторов равен сумме образов слагаемых, образ вектора, умноженного на число, равен произведению этого числа на образ вектора.
Замечание 19.1 В этой главе с каждым линейным преобразованием будет связана матрица, которую мы будем обозначать той же буквой, что и само преобразование. Чтобы их различать, мы для букв, обозначающих преобразование, будем использовать так называемый "каллиграфический" шрифт.
Линейное преобразование пространства  называют также линейным отображением из
называют также линейным отображением из  в
в  или линейным оператором из
или линейным оператором из  в
в  .
.
Исходя из равенств (19.1) легко проверить, что
то есть образ линейной комбинации векторов равен линейной комбинации их образов.
Рассмотрим несколько примеров линейных преобразований.
Пример 19.1 Пусть

-- двумерное векторное пространство, то есть множество векторов плоскости. Пусть
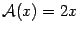
. Это преобразование действует так: каждый вектор оно переводит в вектор такого же направления, но в два раза большей длины. Если считать, что все векторы имеют начало в начале координат, то преобразование

можно представить как растяжение плоскости в два раза (рис. 19.1).
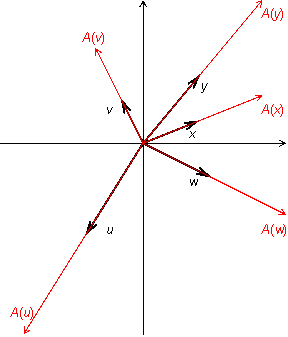
Рис.19.1.Преобразование растяжения
Проверим выполнение равенств (19.1)
Равенства (
19.1) выполнены, следовательно, преобразование

является линейным.
Пример 19.2 Пусть

-- двумерное векторное пространство,

-- поворот вектора по часовой стрелке на угол
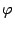
(рис. 19.2).
Рис.19.2.Преобразование поворота
Покажем, что это -- линейное преобразование.
Пусть  и
и 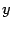 -- два вектора. Тогда
-- два вектора. Тогда 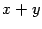 -- это диагональ параллелограмма со стронами
-- это диагональ параллелограмма со стронами 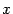 ,
, 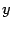 (рис. 19.3).
(рис. 19.3).
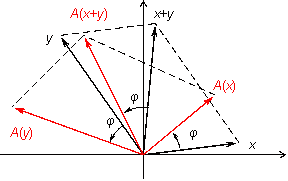
Рис.19.3.Образ суммы векторов
Если параллелограмм повернуть как единое целое на угол 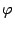 , то его стороны станут векторами
, то его стороны станут векторами 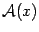 и
и 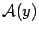 , диагональ будет вектором
, диагональ будет вектором 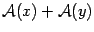 . С другой стороны, диагональ тоже повернулась на угол
. С другой стороны, диагональ тоже повернулась на угол 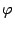 и поэтому является вектором
и поэтому является вектором 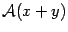 . Следовательно,
. Следовательно, 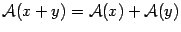 , первое из условий (19.1) выполнено.
, первое из условий (19.1) выполнено.
Пусть 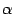 -- число. Из рисунка 19.4 очевидно, что
-- число. Из рисунка 19.4 очевидно, что 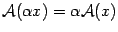 .
.
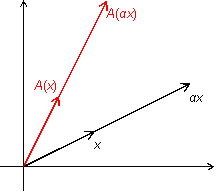
Рис.19.4.Образ вектора, умноженного на число
Следовательно, преобразование

-- линейное.
Упражнение19.1.1. Пусть  -- двумерное векторное пространство,
-- двумерное векторное пространство,  -- некоторая прямая, проходящая через начало координат,
-- некоторая прямая, проходящая через начало координат,  -- преобразование, переводящее каждый вектор
-- преобразование, переводящее каждый вектор 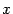 в вектор
в вектор 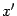 симметричный исходному относительно прямой
симметричный исходному относительно прямой 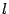 (рис. 19.5). Другими словами,
(рис. 19.5). Другими словами, 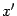 является зеркальным отражением вектора
является зеркальным отражением вектора 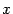 в прямой
в прямой 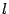 .
.
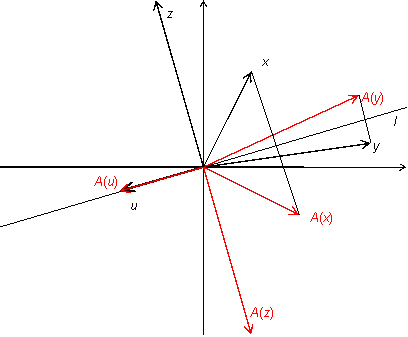
Рис.19.5.Преобразование отражения
Докажите, что  является линейным преобразованием.
является линейным преобразованием.
Упражнение19.1.2. Пусть  -- двумерное векторное пространство,
-- двумерное векторное пространство, 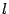 -- некоторая прямая, проходящая через начало координат,
-- некоторая прямая, проходящая через начало координат,  -- преобразование, переводящее каждый вектор
-- преобразование, переводящее каждый вектор 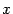 в его проекцию на прямую
в его проекцию на прямую 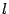 (рис. 19.6).
(рис. 19.6).
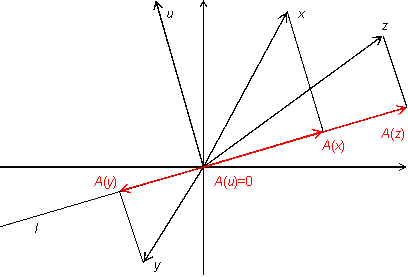
Рис.19.6.Преобразование проектирования
Докажите, что  является линейным преобразованием.
является линейным преобразованием.
Пример 19.3 Пусть

-- пространство всех многочленов,

-- преобразование, которое переводит вектор из

, то есть многочлен, в производную этого многочлена, которая естественно является многочленом, то есть вектором из

. Пусть
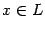
, то есть
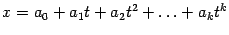
. Тогда
Например, если
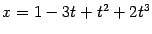
, то
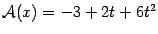
. Покажем, что преобразование

является линейным.
Пусть 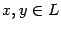 ,
, 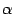 -- число. Тогда в силу свойства линейности производной получим
-- число. Тогда в силу свойства линейности производной получим
Аналогично,
Следовательно,

-- линейное преобразование.
Пример 19.4 Пусть

--

-мерное линейное пространство, Выберем в этом пространстве базис
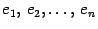
. Тогда у любого вектора
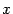
есть его координатный столбец
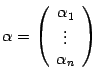
. Пусть
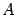
-- квадратная матрица порядка

. Определим преобразование

следующим образом:
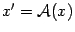
является вектором, координатный столбец которого равен
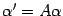
(справа стоит произведение матрицы
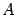
на столбец
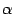
). Покажем, что преобразование

-- линейное.
Пусть 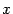 и
и 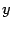 имеют координатные столбцы
имеют координатные столбцы 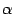 и
и 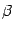 соответственно, а их образы
соответственно, а их образы 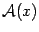 и
и 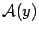 -- координатные столбцы
-- координатные столбцы 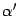 , и
, и 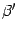 . Тогда
. Тогда
Но выражение в последнем равенстве справа является координатным столбцом образа суммы векторов
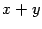
. Следовательно,
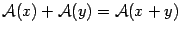
.
Пусть 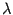 -- произвольное число. Тогда координатный столбец вектора
-- произвольное число. Тогда координатный столбец вектора 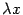 равен
равен 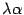 , координатный столбец образа вектора
, координатный столбец образа вектора
то есть равен числу
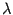
, умноженному на координатный столбец образа вектора
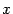
. Поэтому
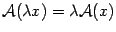
. Тем самым мы доказали, что преобразование

является линейным.
Очевидно, что примерами линейных преобразований могут служить тождественное преобразование, то есть преобразование, переводящее каждый вектор в себя, 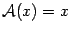 , и нулевое преобразование, переводящее каждый вектор в нуль,
, и нулевое преобразование, переводящее каждый вектор в нуль, 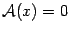 .
.
Легко проверяется, что для любого линейного преобразования  образ нуля равен нулю,
образ нуля равен нулю, 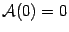 . Действительно, в силу второго из равенств (19.1)
. Действительно, в силу второго из равенств (19.1)
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
![]() называют также линейным отображением из
называют также линейным отображением из ![]() в
в ![]() или линейным оператором из
или линейным оператором из ![]() в
в ![]() .
. 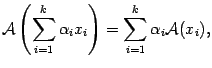


![]() и
и ![]() -- два вектора. Тогда
-- два вектора. Тогда ![]() -- это диагональ параллелограмма со стронами
-- это диагональ параллелограмма со стронами ![]() ,
, ![]() (рис. 19.3).
(рис. 19.3). 
![]() , то его стороны станут векторами
, то его стороны станут векторами ![]() и
и ![]() , диагональ будет вектором
, диагональ будет вектором ![]() . С другой стороны, диагональ тоже повернулась на угол
. С другой стороны, диагональ тоже повернулась на угол ![]() и поэтому является вектором
и поэтому является вектором ![]() . Следовательно,
. Следовательно, ![]() , первое из условий (19.1) выполнено.
, первое из условий (19.1) выполнено. ![]() -- число. Из рисунка 19.4 очевидно, что
-- число. Из рисунка 19.4 очевидно, что ![]() .
. 
![]() -- двумерное векторное пространство,
-- двумерное векторное пространство, ![]() -- некоторая прямая, проходящая через начало координат,
-- некоторая прямая, проходящая через начало координат, ![]() -- преобразование, переводящее каждый вектор
-- преобразование, переводящее каждый вектор ![]() в вектор
в вектор ![]() симметричный исходному относительно прямой
симметричный исходному относительно прямой ![]() (рис. 19.5). Другими словами,
(рис. 19.5). Другими словами, ![]() является зеркальным отражением вектора
является зеркальным отражением вектора ![]() в прямой
в прямой ![]() .
. 
![]() является линейным преобразованием.
является линейным преобразованием. ![]() -- двумерное векторное пространство,
-- двумерное векторное пространство, ![]() -- некоторая прямая, проходящая через начало координат,
-- некоторая прямая, проходящая через начало координат, ![]() -- преобразование, переводящее каждый вектор
-- преобразование, переводящее каждый вектор ![]() в его проекцию на прямую
в его проекцию на прямую ![]() (рис. 19.6).
(рис. 19.6). ![]() является линейным преобразованием.
является линейным преобразованием. ![]() ,
, ![]() -- число. Тогда в силу свойства линейности производной получим
-- число. Тогда в силу свойства линейности производной получим 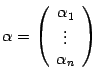 . Пусть
. Пусть ![]() и
и ![]() имеют координатные столбцы
имеют координатные столбцы ![]() и
и ![]() соответственно, а их образы
соответственно, а их образы ![]() и
и ![]() -- координатные столбцы
-- координатные столбцы ![]() , и
, и ![]() . Тогда
. Тогда ![]() -- произвольное число. Тогда координатный столбец вектора
-- произвольное число. Тогда координатный столбец вектора ![]() равен
равен ![]() , координатный столбец образа вектора
, координатный столбец образа вектора ![]() , и нулевое преобразование, переводящее каждый вектор в нуль,
, и нулевое преобразование, переводящее каждый вектор в нуль, ![]() .
. ![]() образ нуля равен нулю,
образ нуля равен нулю, ![]() . Действительно, в силу второго из равенств (19.1)
. Действительно, в силу второго из равенств (19.1) 