‹-- Назад В разделе
"Матрица линейного преобразования" мы выяснили, что каждое линейное преобразование

-мерного линейного пространства в фиксированном базисе задается матрицей. Если меняется базис, то, как правило, меняется и матрица. Возникает вопрос, нельзя ли найти базис, в котором матрица линейного преобразования имеет наиболее простой вид. В общем случае выбрать такой базис довольно сложно. Это связано с нахождением
нормальной жордановой формы матрицы, изложение которого можно найти в более обстоятельных учебниках по линейной алгебре, например, в
[4],
[5]. Следующая теорема отвечает на этот вопрос в более простом случае.
Доказательство. Пусть преобразование  имеет
имеет  линейно независимых собственных векторов
линейно независимых собственных векторов 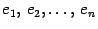 , соответствующих собственным числам
, соответствующих собственным числам 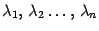 . Так как векторы
. Так как векторы 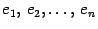 линейно независимы, то они образуют базис. Найдем матрицу преобразования
линейно независимы, то они образуют базис. Найдем матрицу преобразования  в этом базисе. Ее первый столбец является координатным столбцом вектора
в этом базисе. Ее первый столбец является координатным столбцом вектора 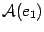 . Так как
. Так как 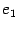 -- собственный вектор, то
-- собственный вектор, то
Координатный столбец этого вектора

. Второй столбец матрицы
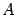
является координатным столбцом вектора
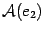
. Так как
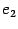
-- собственный вектор, то
Координатный столбец этого вектора

. Вычисляя аналогично остальные столбцы, получаем, что матрица линейного преобразования

в базисе
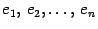
имеет вид (
19.5). Первая часть теоремы доказана.
Пусть в некотором базисе 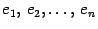 матрица линейного преобразования имеет вид (19.5). Найдем образ вектора
матрица линейного преобразования имеет вид (19.5). Найдем образ вектора 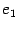 . Этот вектор имеет координатный столбец
. Этот вектор имеет координатный столбец 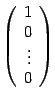 , его образ имеет координатный столбец
, его образ имеет координатный столбец
Следовательно,
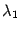
-- собственное число преобразования

, а
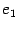
-- соответствущий ему собственный вектор. Аналогично находим, что любой базисный вектор
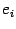
является собственным вектором преобразования

, соответствующим собственному числу
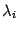
.
Следствие 19.2 Если у матрицы 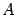 порядка
порядка  существует набор из
существует набор из  линейно независимых собственнных векторов, соответствующих собственным числам
линейно независимых собственнных векторов, соответствующих собственным числам 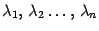 , то матрица
, то матрица 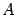 подобна диагональной матрице с числами
подобна диагональной матрице с числами 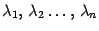 на диагонали.
на диагонали.
Теорема 19.3 Пусть собственные векторы 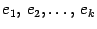 преобразования
преобразования  соответствуют собственным числам
соответствуют собственным числам 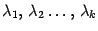 , среди которых нет равных друг другу. Тогда система векторов
, среди которых нет равных друг другу. Тогда система векторов 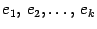 является линейно независимой.
является линейно независимой. Доказательство. Воспользуемся методом математической индукции по числу векторов. Если 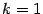 , то утверждение теоремы следует из того, что собственный вектор -- ненулевой.
, то утверждение теоремы следует из того, что собственный вектор -- ненулевой.
Пусть утверждение верно для системы векторов 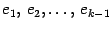 . Составим линейную комбинацию векторов
. Составим линейную комбинацию векторов 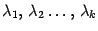 и приравняем ее к нулю
и приравняем ее к нулю
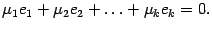 | (19.6) |
К обеим частям применим преобразование

По определению линейного преобразования получим
Так как
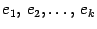
-- собственные векторы, то
Умножим равенство (
19.6) на
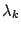
и вычтем из последнего равенства. Получим
Так как по предположению индукции векторы
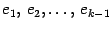
линейно независимы, то
По условию
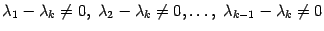
, следовательно,
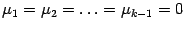
. Подставим эти значения в (
19.6), получим
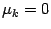
. Получили, что из равенства (
19.6) следует
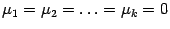
, то есть векторы
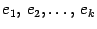
линейно независимы.
Следствие 19.3 Если матрица 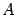 порядка
порядка  имеет
имеет  попарно различных собственных чисел, то она подобна диагональной матрице.
попарно различных собственных чисел, то она подобна диагональной матрице.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
![]() имеет
имеет ![]() линейно независимых собственных векторов
линейно независимых собственных векторов ![]() , соответствующих собственным числам
, соответствующих собственным числам ![]() . Так как векторы
. Так как векторы ![]() линейно независимы, то они образуют базис. Найдем матрицу преобразования
линейно независимы, то они образуют базис. Найдем матрицу преобразования ![]() в этом базисе. Ее первый столбец является координатным столбцом вектора
в этом базисе. Ее первый столбец является координатным столбцом вектора ![]() . Так как
. Так как ![]() -- собственный вектор, то
-- собственный вектор, то  . Второй столбец матрицы
. Второй столбец матрицы  . Вычисляя аналогично остальные столбцы, получаем, что матрица линейного преобразования
. Вычисляя аналогично остальные столбцы, получаем, что матрица линейного преобразования ![]() матрица линейного преобразования имеет вид (19.5). Найдем образ вектора
матрица линейного преобразования имеет вид (19.5). Найдем образ вектора ![]() . Этот вектор имеет координатный столбец
. Этот вектор имеет координатный столбец 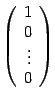 , его образ имеет координатный столбец
, его образ имеет координатный столбец 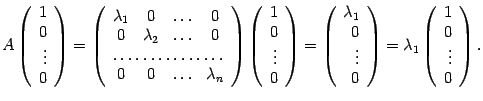
![]() , то утверждение теоремы следует из того, что собственный вектор -- ненулевой.
, то утверждение теоремы следует из того, что собственный вектор -- ненулевой. ![]() . Составим линейную комбинацию векторов
. Составим линейную комбинацию векторов ![]() и приравняем ее к нулю
и приравняем ее к нулю