‹-- Назад
Метод почти половинного деления
Пусть 
-- непрерывная функция, точку минимума которой на отрезке 
мы хотим найти с точностью 
. В этом методе мы предполагаем, что 
-- единственная точка локального минимума функции на отрезке . Мы будем последовательно сужать отрезок 
так, чтобы точка минимума 
всегда оставалась на выбираемой части отрезка 
, и продолжим процедуру до тех пор, пока длина 
оставшейся части отрезка не станет меньше 
. После этого достаточно будет взять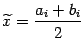 
, и очевидно, что тогда будет 
, то есть точка будет найдена с требуемой точностью.
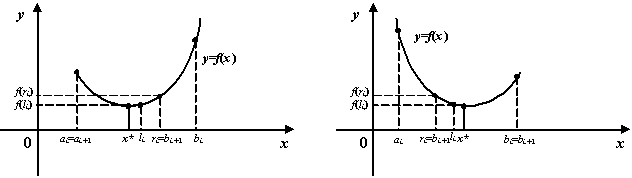
Опишем теперь процесс выбора той части 
отрезка , на которой находится точка минимума . Выбор конечных точек 
и 
будет использовать значения функции в концах предыдущего отрезка, то есть 
и 
.
Перед началом вычисления выберем число 
и положим 
. Шаг перехода от 
к состоит в следующем. Вычислим два значения функции, в точках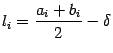 
и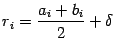 
. Эти две точки симметричны относительно середины отрезка, точки 
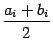. Сравним теперь значения 
и 
:
если 
, то 
, и надо положить 
, то есть взять 
;
если же 
, то 
, и надо положить 
, то есть взять 
(см. следующий чертёж).
На первых итерациях, когда длины отрезков остаются много больше малого числа 
, длина 
нового отрезка меньше длины предыдущего отрезка почти вдвое:
начинает уменьшаться не так быстро и приближается к 
. Поскольку мы выбирали так, что 
, на некотором шаге будет выполнено неравенство 
и, как отмечалось выше, процесс можно будет прервать и взять .
только одна точка локального минимума, то применение описанного выше алгоритма приводит к нахождению какой-то одной из точек локального минимума, причём не обязательно той, в которой принимается наименьшее на всём отрезке значение. Это общая трудность, присущая методам минимизации. Однако на практике, как правило, в оптимизационных задачах обычно из каких-то соображений (часто лежащих вне математики) известно, что на рассматриваемом отрезке других локальных минимумов нет, то есть функция убывает на 
и возрастает на 
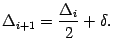
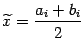; вся проблема только в том, что неизвестно положение точки . Довольно часто существование и единственность локального минимума на является следствием того, что функция строго выпукла на . Тогда, действительно, не может иметь на интервале 
более одной точки локального минимума.
Если же для рассматриваемой функции такие свойства неизвестны, то остаётся действовать эмпирически: применить метод к отрезку и некоторым его частям вида 
, выбранным наугад. Если каждый раз либо будет получаться то же самое значение (с выбранной точностью), либо будет оказываться, что 
, а минимум на больше, чем значение в точке , то значение найдено верно.
