‹-- Назад
Формула понижения степени
Для вычисления интегралов вида
Заметим, что при 
и 
получаются табличные интегралы:
 | |
 |
Выведем формулы, позволяющие свести вычисление
и 
к 
и 
соответственно. Применяя эти формулы к исходным интегралам несколько раз, при чётном 
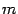
мы сведём дело к вычислению табличного интеграла 
или 
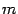
, а при нечётном -- к вычислению табличного интеграла 
или 
. Итак, получим формулу, выражающую через ; эта формула называется формулой понижения степени. Преобразуем интеграл следующим образом:
 | |
 |
Последний интеграл вычислим, применив формулу интегрирования по частям:
 | |
 |
(В комментарии, между вертикальными чёрточками, мы не вполне корректно обозначили через
не полный набор первообразных для 
, а какую-либо, произвольную, первообразную, одну из которых и нашли. Только эта первообразная нам и нужна для дальнейшего. Поэтому произвольную постоянную 
добавлять не стали.) После этого получаем 
Мы получили выражение интеграла
через интеграл и известную функцию. С помощью аналогичных преобразований, для интеграла получаем такое выражение через интеграл и известную функцию:
Как упражнение, выполните эти преобразования и получите приведённую здесь формулу (2.3).
и 
и .
. После однократного применения формулы понижения степени (2.2), дело сведётся к нахождению интеграла 
. Итак,
и подобных ему -- не единственно возможный. Если записать подынтегральное выражение в виде
и 
, то получим равенство
. Первообразные в этих двух ответах тождественно равны друг другу:
