‹-- Назад
Интегралы, сводящиеся к интегралам от рациональных функций
Некоторые типы неопределённых интегралов сводятся путём соответствующей замены к интегралам от рациональных функций. Рассмотрим три таких случая.
рациональным образом зависит от выражения 
, если можно представить в виде
-- рациональная функция от переменного 
. Например, функция
, а функция
. Одночленом от двух переменных и 
назовём выражение вида 
, где 
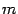, а показатели степени 
и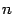 
-- целые неотрицательные числа. Многочленом от двух переменных и назовём сумму конечного числа одночленом от этих двух переменных. (Считаем, что сумма может состоять и из одного слагаемого, так что каждый одночлен -- это частный случай многочлена.)
Например, 
, 
, 
-- многочлены от переменных и .
Рациональной функцией от двух переменных и назовём отношение двух многочленов от и :
и 
-- многочлены от и . Например, функции
-- и .
рациональным образом зависит от выражений и 
, если можно представить в виде
-- рациональная функция от переменных и . Например, функция
и 
, а функция
и 
: нужно взять
Теперь рассмотрим обещанные классы интегралов.
1. Интегралы от функций, рациональным образом зависящих от экспоненты. Рассмотрим интегралы вида
-- рациональная функция. Сделаем естественную замену . Тогда 
и 
. Получаем:
. Заметим, что 
-- это тоже рациональная функция, так как 
-- тоже многочлен. Таким образом, мы свели дело к вычислению интеграла от рациональной функции 
, после нахождения которого нужно сделать замену и получить ответ.
, получаем:
получаем 
, откуда
получаем 
, откуда
: при 
получаем:
--
, 
. Значит, искомое разложение имеет вид
 | |
 | |
 |
принимает постоянные значения. Сколько получается таких промежутков?
2. Интегралы от функций, рациональным образом зависящих от 
и 
.
Рассмотрим интегралы вида
-- рациональная функция от двух переменных и , а выражения и таковы: , 
, и 
. Такие интегралы приводятся к интегралам от рациональных функций одного переменного, если сделать естественную замену . Действительно, тогда 
и 
, а интеграл приводится к виду
рационально зависит от единственного своего аргумента . Заметим, что точно та же замена годится и в случае, когда подынтегральная функция зависит рациональным образом только от .
, поскольку её можно записать в виде
:
которая является неправильной дробью, поскольку степень её числителя, равная 7, больше степени знаменателя, равной 1. Значит, нужно выделить в этой дроби целую часть. Для этого разделим числитель на знаменатель "столбиком":
и остаток 2, значит, неправильная дробь представляется в виде
 | |
 | |
 |
3. Интегралы от функций, рациональным образом зависящих от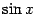 
и 
.
И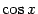нтегралы вида
-- функция, рациональным образом зависящая от и , можно привести к интегралу от рациональной функции от одного переменного 
, если сделать так называемую "универсальную" замену
, откуда
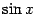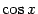-- рациональная функция одного переменного . Если имеет место частный случай рациональной зависимости от и , когда обе эти функции входят в выражение лишь в чётных степенях, то есть подынтегральная функция имеет вид
, откуда
Выполняя замену 
, получаем:
 | |
 |
Если в том же интеграле сделать универсальную замену, то получаем:
 |
Получили интеграл от рациональной функции переменного
. Однако вычисление этого интеграла представляется весьма трудоёмким, поскольку непонятно даже, как искать разложение знаменателя на множители5. Так что первая замена оказалась много лучше второй.
годится также в случае интеграла 
, в котором функция рациональным образом зависит от и и обладает следующим свойством:
зависит от своих аргументов несимметричным образом, то ничего не остаётся делать, как применять не всегда приятную универсальную замену 
.
 | |
 |
В данном примере исходная подынтегральная функция была не столь уж сложна, и универсальная замена сразу привела нас к табличному интегралу.
