‹-- Назад
Пределы при разных условиях. Некоторые частные случаи
Пусть задана некоторая меняющаяся величинаДадим теперь строгие определения предела в некоторых частных случаях, а потом перейдём к обсуждению общего определения.
Пусть ![]() -- это функция вещественного переменного
-- это функция вещественного переменного ![]() , определённая во всех точках интервала
, определённая во всех точках интервала ![]() , кроме, быть может, точки
, кроме, быть может, точки ![]() . Дадим определение предела величины
. Дадим определение предела величины ![]() при условии, что
при условии, что ![]() стремится к точке
стремится к точке ![]() . Это условие кратко обозначается
. Это условие кратко обозначается ![]() . Стремление
. Стремление ![]() к
к ![]() означает, что при своём изменении
означает, что при своём изменении ![]() оказывается во всё более узких окрестностях, окружающих точку
оказывается во всё более узких окрестностях, окружающих точку ![]() , но не совпадает с
, но не совпадает с ![]() , то есть значение
, то есть значение ![]() становится всё меньше и меньше, приближаясь к 0, но нулём не становится. При этом может оказаться, что соответствующие
становится всё меньше и меньше, приближаясь к 0, но нулём не становится. При этом может оказаться, что соответствующие ![]() значения
значения ![]() становятся всё ближе и ближе к некоторому фиксированному числу
становятся всё ближе и ближе к некоторому фиксированному числу ![]() , причём для любой, сколь угодно малой, окрестности числа
, причём для любой, сколь угодно малой, окрестности числа ![]() можно указать, насколько близко
можно указать, насколько близко ![]() должен подойти к
должен подойти к ![]() , чтобы значения
, чтобы значения ![]() уже попадали в эту окрестность числа
уже попадали в эту окрестность числа ![]() . Тогда число
. Тогда число ![]() есть предел функции
есть предел функции ![]() при условии
при условии ![]() , что записывается так:
, что записывается так:
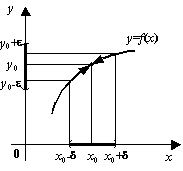
Формализуем сказанное для придания большей математической ясности. Любая окрестность точки ![]() (симметричная относительно
(симметричная относительно ![]() ) характеризуется её полушириной
) характеризуется её полушириной ![]() , то есть имеет вид интервала
, то есть имеет вид интервала ![]() . Если значение
. Если значение ![]() попало в такую
попало в такую ![]() -окрестность, то это означает, что
-окрестность, то это означает, что ![]() . Любая окрестность точки
. Любая окрестность точки ![]() , не содержащая самой точки
, не содержащая самой точки ![]() (и симметричная относительно
(и симметричная относительно ![]() ), -- это объединение двух смежных интервалов3
), -- это объединение двух смежных интервалов3 ![]() . Попадание точки
. Попадание точки ![]() в эту окрестность означает, что выполнено неравенство
в эту окрестность означает, что выполнено неравенство ![]() и
и ![]() . Равенство
. Равенство ![]() означает тогда, что
означает тогда, что
для любого, сколь угодно малого, числа ![]() можно найти такое число
можно найти такое число ![]() (зависящее от
(зависящее от ![]() ), что при
), что при ![]() будет
будет ![]() .
.
При этом число ![]() называется пределом функции
называется пределом функции ![]() при условии
при условии ![]() . Тот факт, что
. Тот факт, что ![]() , записывают ещё в виде
, записывают ещё в виде
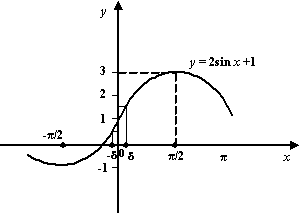
Попадание значений ![]() в окрестность
в окрестность ![]() означает, что выполняется неравенство
означает, что выполняется неравенство ![]() , то есть
, то есть ![]() . При этом нас интересуют только те решения этого неравенства, которые лежат вблизи точки
. При этом нас интересуют только те решения этого неравенства, которые лежат вблизи точки ![]() . Решая неравенство, получаем, что оно выполняется при
. Решая неравенство, получаем, что оно выполняется при ![]() . Таким образом, если взять
. Таким образом, если взять ![]() (это число больше 0), то при
(это число больше 0), то при ![]() будет выполнено неравенство
будет выполнено неравенство ![]() , что и означает, что предел равен числу 1:
, что и означает, что предел равен числу 1: ![]() , или
, или ![]() .
.
Рассмотрим теперь другой важный случай предела.
Пусть дана бесконечная последовательность ![]() чисел, занумерованных по порядку:
чисел, занумерованных по порядку:
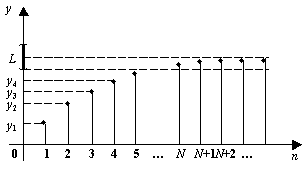
Формализуем сказанное. Множества чисел ![]() , заданные условиями
, заданные условиями ![]() , можно назвать окрестностями бесконечности. Равенство
, можно назвать окрестностями бесконечности. Равенство ![]() означает тогда, что
означает тогда, что
для любого, сколь угодно малого, числа ![]() можно найти такое число
можно найти такое число ![]() (зависящее от
(зависящее от ![]() ), что при
), что при ![]() (то есть в достаточно далёкой окрестности бесконечности будет выполняться неравенство
(то есть в достаточно далёкой окрестности бесконечности будет выполняться неравенство ![]() .
.
При этом число ![]() называется пределом последовательности
называется пределом последовательности ![]() при условии
при условии ![]() . Тот факт, что
. Тот факт, что ![]() , записывают также в виде
, записывают также в виде
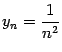 равен 0.
равен 0. 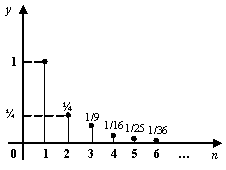
Фиксируем произвольное число ![]() и подберём число
и подберём число ![]() в зависимости от
в зависимости от ![]() так, чтобы при
так, чтобы при ![]() выполнялось неравенство
выполнялось неравенство ![]() , то есть
, то есть 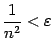 . Решая это неравенство, получаем, что оно выполняется при
. Решая это неравенство, получаем, что оно выполняется при 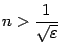 . Значит, достаточно выбрать в качестве
. Значит, достаточно выбрать в качестве ![]() натуральное число, ближайшее к
натуральное число, ближайшее к ![]() справа на вещественной оси4, то есть
справа на вещественной оси4, то есть 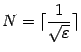 , и тогда при любом
, и тогда при любом ![]() неравенство
неравенство 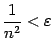 будет верным. Это означает, что
будет верным. Это означает, что
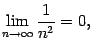
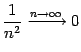 .
. Совершенно аналогично определению предела последовательности выглядит следующее определение.
Определим окрестности бесконечности как множества точек ![]() , заданные неравенствами
, заданные неравенствами ![]() , то есть лучи
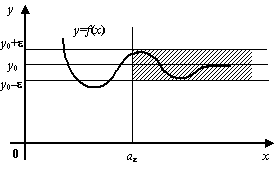
, то есть лучи ![]() . Потребуем, чтобы для любой, сколь угодно малой, окрестности
. Потребуем, чтобы для любой, сколь угодно малой, окрестности ![]() точки
точки ![]() можно было найти такую окрестность бесконечности
можно было найти такую окрестность бесконечности ![]() , что при попадании
, что при попадании ![]() в эту окрестность, то есть при
в эту окрестность, то есть при ![]() , соответствующее значение
, соответствующее значение ![]() попадает в заданную вначале окрестность точки
попадает в заданную вначале окрестность точки ![]() , то есть выполняется неравенство
, то есть выполняется неравенство ![]() . Выполнение этого требования будет означать, что
. Выполнение этого требования будет означать, что ![]() -- предел функции
-- предел функции ![]() при условии
при условии ![]() , то есть
, то есть
Тот факт, что ![]() , записывают ещё в виде
, записывают ещё в виде
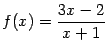 при
при 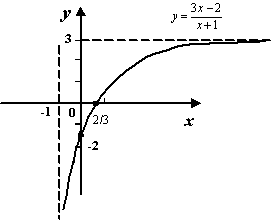
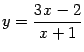
Фиксируем ![]() и подберём по этому числу
и подберём по этому числу ![]() такое число
такое число ![]() , что при любом
, что при любом ![]() выполняется неравенство
выполняется неравенство
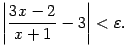
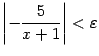 или
или 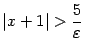 . Так как
. Так как 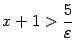 , откуда
, откуда 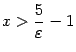 . Если теперь взять число
. Если теперь взять число 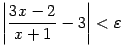 ; это означает, что
; это означает, что 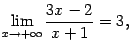
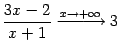 .
.
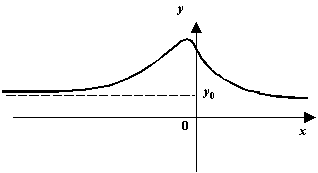
Пользуясь этим определением, покажите, что 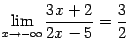 .
.