mathserfer.narod.ru

Теория по высшей математике

‹-- Назад

Интегралы от функций, рациональным образом зависящих от и

Пусть функция рациональным образом зависит от своих аргументов и . Рассмотрим интеграл

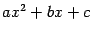
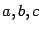
где квадратный трёхчлен содержит по крайней мере два ненулевых слагаемых, и (  -- некоторые постоянные). Будем считать, что он не равен полному квадрату некоторого линейного выражения, то есть

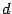
где ( и  -- некоторые постоянные), так как иначе квадратный корень извлекается: , и интеграл сводится к интегралу от рациональной функции переменного (при и при получаются разные интегралы!). При этом предположении мы можем выделить в этом квадратном трёхчлене полный квадрат и привести его к одному из трёх возможных видов:
1) ;
2) ;
3) ,
где  -- некоторая постоянная, а  -- линейное выражение. (Четвёртый логически возможный случай, , означает, что под корнем находится отрицательное выражение, и поэтому рассматриваться не будет.)

Подберём такие тригонометрические замены, чтобы корень извлекался. В первом случае, когда подкоренное выражение равно , годится замена , где  -- некоторая новая переменная. Тогда

Достаточно считать, что , так как при этом переменная принимает все возможные для неё значения . Тогда и . Получаем, что

и

Переходя к новой переменной в интеграле, получим:

где  -- некоторая функция, рациональным образом зависящая от синуса и косинуса. Тем самым вычисление интеграла свелось к уже изученному выше случаю.

Во втором случае, когда подкоренное выражение равно , сделаем замену . Тогда

Достаточно считать, что , так как при этом переменная принимает все возможные значения . Тогда и . Интеграл приводится к виду

где  -- некоторая функция, рациональным образом зависящая от синуса и косинуса. Снова вычисление интеграла свелось к изученному случаю.

Наконец, в третьем случае, когда подкоренное выражение равно , сделаем замену . Тогда

Достаточно считать, что , так как тогда принимает все допустимые значения . Интеграл приводится к виду

где  -- некоторая функция, рациональным образом зависящая от синуса и косинуса⁶. И опять вычисление интеграла свелось к изученному случаю.

Во многих случаях предложенные замены -- не единственно возможные и даже, быть может, не самые удачные. Найденный только что интеграл можно было бы вычислить, например, с помощью иной замены, ; эта замена годится для вычисления всех интегралов вида . Предварительно преобразуем интеграл следующим образом:

Заметим, что поскольку и , имеем . Рассматривая случай , когда , получаем интеграл

а в случае , когда , получаем интеграл

В итоге получаем

Заметим, что в примере полученный ответ имел (формально) другой вид. Однако напомним, что найденные разными способами первообразные могут различаться на постоянное слагаемое на каждом из интервалов области определения; кроме того, не следует забывать про возможность тождественных преобразований, особенно когда речь идёт о тригонометрических выражениях.