mathserfer.narod.ru

        Пример 2.21   Вычислим интеграл

Поскольку синус стоит в нечётной положительной степени, то следует отделить от этой степени один множитель и объединить со знаком дифференциала, после чего всё подынтегральное выражение можно будет выразить через :

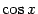
где была использована замена .     

        Пример 2.22   Вычислим интеграл

двумя способами:
а) с помощью понижения степени и
б) применяя формулу и делая замену . Покажем, что оба способа приводят к одной и той же первообразной, записанной двумя различными способами.

а). Формула понижения степени при даёт:

а при  --

Заметим, что

Объединяя эти формулы, получаем:

б). Преобразовываем интеграл так:

Теперь покажем, что на самом деле выражения в ответах тождественно равны:

    

        Пример 2.23   Вычислим интеграл

Дробь  -- неправильная, поскольку степень числителя равна степени знаменателя. Поэтому нужно выделить целую часть. Это в данном примере проще сделать без деления столбиком:

При последнем преобразовании мы еще и разложили знаменатель на множители. Теперь разложим получившуюся правильную дробь в сумму простейших дробей. Это разложение будет иметь вид

Для нахождения и приведём сумму в правой части к общему знаменателю и приравняем числители:

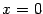
Подставляя , получаем:

откуда . Подставляя , получаем:

откуда . Наконец, подставляя , получаем:

откуда Итак, получаем, что

Теперь можно вычислить интеграл:

Ответ:     

        Пример 2.24   Найдём интеграл

Подынтегральная функция является рациональной относительно и , значит, для вычисления интеграла нужно сделать замену :

Разделим числитель на знаменатель столбиком:

Получили целую часть и остаток . Значит,

Подставляя это выражение под знак интеграла, получаем:

Осталось вернуться к исходной переменной : поскольку , получаем:

    

Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции