mathserfer.narod.ru

Теория по высшей математике

‹-- Назад

Проверка геометрического смысла интеграла при подсчёте площади части круга

Напомним, что выше мы проверили, что формула

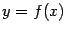
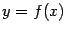
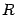
действительно даёт площадь трапеции, давно нам известную в том случае, когда линия  -- прямая. Мы заметили, что надо еще проверить, что эта формула не противоречит другому издавна известному нам случаю площади: когда линия  -- часть окружности, то эту площадь можно подсчитать, исходя из формулы для площади круга (напомним, она равна для круга радиуса ). 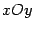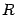Не ограничивая общности, можно считать, что центр круга совпадает с началом координат координатной плоскости , так что окружность радиуса имеет уравнение

Верхняя полуокружность задана тогда уравнением , то есть представляет собой график функции .

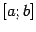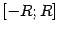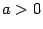Пусть теперь взят отрезок , целиком умещаюшийся на диаметре , лежащем на оси . Для определённости разберём случай, когда (тогда ). Проведём вертикальные отрезк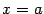и и 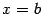через концы 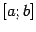до пересечения с полуокружностью и получим криволинейную трапецию. Для подсчёта её площади геометрическим способом проведём радиусы и в точки пересечения вертикальных отрезков 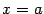и 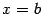, соответственно, с полуокружностью. Длины этих вертикальных отрезков равны и . Площадь треугольника равна, очевидно, , а площадь треугольника равна . Радиус проведён под углом к оси , а радиус  -- под углом к оси . Используя формулу площади сектора с центральным углом , находим площадь сектора круга :

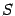
Поскольку, как видно из чертежа, площадь криволинейной трапеции равна

то получаем формулу

Наша задача -- проверить, что к той же самой формуле приводят и правила интегрирования, если площадь криволинейной трапеции подсчитывать по общей фоpмуле площади области, лежащей под гpафиком функции , то есть вычислять как

Итак, приступаем к преобразованию этого интеграла. Первым делом проинтегрируем по частям:

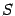
После интегрирования по частям мы преобразовали интеграл в правой части, добавив и отняв в числителе, после чего поделили скобку на и получили тот же интеграл, с которого начинали, то есть . Оставшийся интеграл

табличный, но вместо привычной табличной формулы

мы воспользовались (тоже верной) формулой

и применили формулу Ньютона - Лейбница для вычисления определённого интеграла. Теперь в полученном равенстве

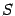
перенесём из правой части в левую и поделим обе части пополам. Получим:

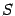
Это та же самая формула для площади , что была получена выше, исходя из формулы площади кругового сектора. Значит, способ подсчёта площади с помощью интеграла не противоречит и этой формуле площади, известной из элементарной геометрии.