‹-- Назад
Непрерывность обратной функции
Пусть 
-- функция, непрерывная на отрезке 
. Предположим, что монотонна на ; пусть, для определённости, она монотонно возрастает: из 
следует, что 
. Тогда образом отрезка будет отрезок 
, где 
и 
(действительно, непрерывная функция принимает любое промежуточное между 
и 
значение, причём ровно один раз, что следует из монотонности). Поэтому существует обратная к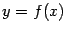 
функция 
функция, действующая из в . Очевидно, что 
монотонно возрастает. (Если бы функция 
была монотонно убывающей, то и обратная к ней функция тоже была бы монотонно убывающей.)
-- непрерывная монотонная функция, 
, 
. Тогда обратная к функция непрерывна на отрезке . Доказательство. Во-первых, заметим, что если 
, 
, то 
.
Во-вторых, пусть 
; рассмотрим функцию 
, которая определена при 
. Очевидно, что 
-- непрерывная на 
функция, поэтому она принимает наименьшее значение 
в некоторой точке 
:
, то 
, то есть если 
, то 
. Последнее утверждение можно переформулировать так: для любого числа 
найдётся число 
, такое что при 
выполняется неравенство 
. (При этом 
, 
, 
, 
.) Получили, что функция удовлетворяет определению равномерной непрерывности на отрезке ; тем самым доказано утверждение теоремы.
