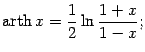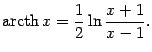‹-- Назад
Гиперболические функции и ареа-функции
Для рассмотрения дальнейших примеров нам понадобится определение гиперболических функций и ареа-функций, обратных к гиперболическим.
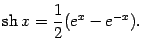
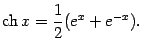
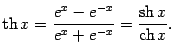
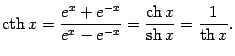
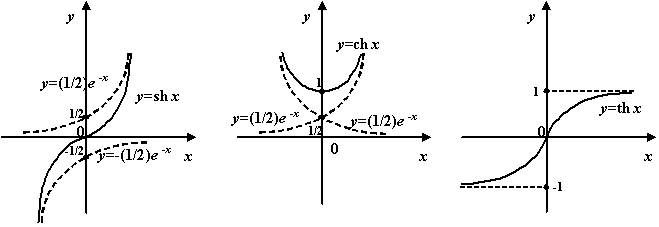
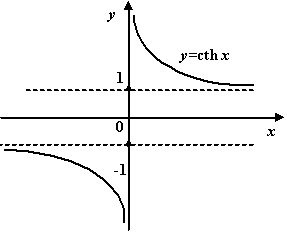
Функции ![]() ,
, ![]() и
и ![]() -- нечётные; функция
-- нечётные; функция ![]() -- чётная. Области определения гиперболических функций таковы:
-- чётная. Области определения гиперболических функций таковы:
Некоторые из свойств гиперболических функций схожи (но не всегда в точности совпадают) со свойствами соответствующих тригонометрических функций. Например, имеют место формулы:
и многие другие формулы, аналогичные известным формулам тригонометрии.
Подобно тому, как равенство ![]() выражает тот факт, что точка координатной плоскости
выражает тот факт, что точка координатной плоскости ![]() с координатами
с координатами ![]() ,
, ![]() при изменении параметра
при изменении параметра ![]() движется по окружности радиуса 1, заданной уравнением
движется по окружности радиуса 1, заданной уравнением ![]() (и называемой тригонометрическим кругом), равенство
(и называемой тригонометрическим кругом), равенство ![]() говорит о том, что точка с координатами
говорит о том, что точка с координатами ![]() ,
, ![]() движется по равносторонней гиперболе, заданной уравнением
движется по равносторонней гиперболе, заданной уравнением ![]() . Отсюда и происходит название: гиперболические функции.
. Отсюда и происходит название: гиперболические функции.
Функции ![]() ,
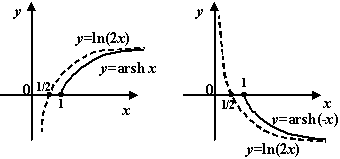
, ![]() непрерывны и монотонно возрастают на своих областях определения. Поэтому они имеют обратные функции, которые также монотонно возрастают и непрервыны. Функция, обратная к функции
непрерывны и монотонно возрастают на своих областях определения. Поэтому они имеют обратные функции, которые также монотонно возрастают и непрервыны. Функция, обратная к функции ![]() , называется обратным гиперболическим синусом, или ареа-синусом, и обозначается
, называется обратным гиперболическим синусом, или ареа-синусом, и обозначается ![]() . Имеем:
. Имеем: ![]() ,
, ![]() . Функция, обратная к функции
. Функция, обратная к функции ![]() , называется обратным гиперболическим тангенсом, или ареа-тангенсом, и обозначается
, называется обратным гиперболическим тангенсом, или ареа-тангенсом, и обозначается ![]() . Итак,
. Итак, ![]() ,
, ![]() .
.
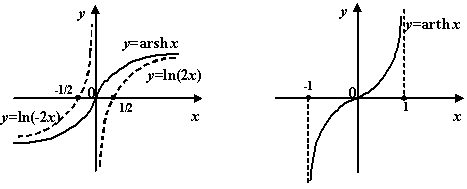
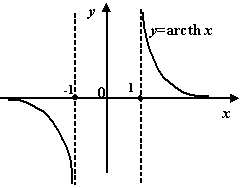
Функция ![]() , хотя и имеет разрыв в точке 0, монотонна на интервалах
, хотя и имеет разрыв в точке 0, монотонна на интервалах ![]() и
и ![]() и принимает каждое своё значение ровно один раз. Поэтому существует обратная функция, называемая обратным гиперболическим котангенсом, или ареа-котангенсом, обозначаемая
и принимает каждое своё значение ровно один раз. Поэтому существует обратная функция, называемая обратным гиперболическим котангенсом, или ареа-котангенсом, обозначаемая ![]() . Она определена на
. Она определена на ![]() и принимает значения в множестве
и принимает значения в множестве ![]() .
.
Функция ![]() не является монотонной на всей своей области определения. Однако монотонно (и непрерывно) её ограничение на полуось
не является монотонной на всей своей области определения. Однако монотонно (и непрерывно) её ограничение на полуось ![]() , при этом функция
, при этом функция ![]() принимает все значения из
принимает все значения из ![]() . Поэтому для этого ограничения существует обратная функция, называемая обратным гиперболическим косинусом, или ареа-косинусом и обозначаемая
. Поэтому для этого ограничения существует обратная функция, называемая обратным гиперболическим косинусом, или ареа-косинусом и обозначаемая ![]() . Она непрерывна на своей области определения
. Она непрерывна на своей области определения ![]() и принимает значения на
и принимает значения на ![]() .
.
Возможен вариант: вместо ограничения на ![]() можно рассмотреть ограничение функции
можно рассмотреть ограничение функции ![]() на
на ![]() , а затем функцию, обратную к этому ограничению. Эту функцию часто также называют ареа-косинусом и обозначают
, а затем функцию, обратную к этому ограничению. Эту функцию часто также называют ареа-косинусом и обозначают ![]() , однако нужно чётко осознавать, что при таком построении получается другая функция (будем обозначать её здесь
, однако нужно чётко осознавать, что при таком построении получается другая функция (будем обозначать её здесь ![]() ). Итак,
). Итак, ![]() и
и ![]() .
.