‹-- Назад
Определение 13.6 Конусом второго порядка называется поверхность, уравнение которой в некоторой декартовой системе координат имеет вид
 | (13.10) |
где

,

,

-- положительные числа.
Замечание 13.1 С математической точки зрения поверхность (
13.10) лучше определять с помощью уравнения
 | (13.11) |
так как в нем меньше параметров, но при этом, во-первых, теряется аналогия с уравнениями предыдущих поверхностей, а во-вторых, если считать, что величины

,

,
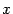
,
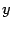
,
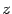
имеют размерность длины, то в уравнении (
13.11) размерности правой и левой части не согласуются.
Для краткости в дальнейшем конус второго порядка будем называть просто конус. Исследуем форму конуса. Так же, как эллипсоид и гиперболоиды, он имеет три плоскости симметрии, три оси симметрии и центр симметрии. Ими являются соответственно координатные плоскости, координатные оси и начало координат.
Для построения конуса найдем его сечения различными плоскостями. Найдем линию пересечения с плоскостью 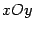 . На этой плоскости
. На этой плоскости  , поэтому
, поэтому
Координаты только одной точки плоскости
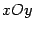
могут удовлетворять данному уравнению, а именно, начала координат. Найдем линию пересечения с плоскостью

. На этой плоскости

, поэтому
Это уравнение пары прямых

на плоскости

. Построим эти прямые (рис. 13.16). Сечение плоскостью

также является парой прямых с уравнением

. Нарисуем и эти прямые (рис. 13.16).

Рис.13.16.Сечения конуса координатными плоскостями Найдем линии пересечения поверхности с плоскостями  ,
,  . Уравнения этих линий
. Уравнения этих линий
Первое уравнение преобразуем к виду
то есть к виду
 | (13.12) |
где

,

. Уравнение (
13.12) является уравнением эллипса. Нарисуем полученные сечения (рис. 13.17).

Рис.13.17.Изображение конуса с помощью сечений Привычное для глаза изображение приведено на рисунке 13.18.

Рис.13.18.Конус Точка пересечения конуса с плоскостью 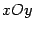 называется вершиной конуса.
называется вершиной конуса.
Если в уравнении (13.10)  , то сечения конуса плоскостями параллельными плоскости
, то сечения конуса плоскостями параллельными плоскости 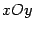 являются окружностями. В этом случае поверхность называется прямым круговым конусом и может быть получена вращением прямой, лежащей в плоскости
являются окружностями. В этом случае поверхность называется прямым круговым конусом и может быть получена вращением прямой, лежащей в плоскости  , вокруг оси
, вокруг оси 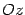 . Именно с таким конусом мы имеем дело в школьном курсе математики.
. Именно с таким конусом мы имеем дело в школьном курсе математики.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
![]() . На этой плоскости
. На этой плоскости ![]() , поэтому
, поэтому 


![]() ,
, ![]() . Уравнения этих линий
. Уравнения этих линий 



![]() называется вершиной конуса.
называется вершиной конуса. ![]() , то сечения конуса плоскостями параллельными плоскости
, то сечения конуса плоскостями параллельными плоскости ![]() являются окружностями. В этом случае поверхность называется прямым круговым конусом и может быть получена вращением прямой, лежащей в плоскости
являются окружностями. В этом случае поверхность называется прямым круговым конусом и может быть получена вращением прямой, лежащей в плоскости ![]() , вокруг оси
, вокруг оси ![]() . Именно с таким конусом мы имеем дело в школьном курсе математики.
. Именно с таким конусом мы имеем дело в школьном курсе математики.


