‹-- Назад
Площадь области, лежащей между двумя графиками
Пусть
и 
-- две непрерывные функции, заданные на отрезке 
, причём 
при всех 
. Между графиками 
и 
лежит область 
, с боков ограниченная отрезками прямых 
и 
. 
Рис.6.1.
Если обе функции неотрицательны, то есть
, то для вычисления площади 
области достаточно заметить, что она равна разности площадей областей 
и 
, лежащих между отрезком (снизу) и, соответственно, графиком и (сверху). Для нахождения площади 
области и 
области применим формулу (6.1) и получим: 
Если же неравенство не выполнено, то заметим следующее: функция ограничена, в том числе снизу, на :
(по предположению, 
). Сдвинем оба графика, и , на 
единиц вверх, то есть рассмотрим функции 
и 
. Тогда, с одной стороны, область между графиками тоже целиком сдвигается на 
вверх, и её площадь не изменяется; с другой стороны, оба сдвинутых вверх графика окажутся целиком не ниже оси 
, и площадь между ними можно будет сосчитать по формуле (6.2). Заметим теперь, что
и расположены относительно оси .
Пример 6.1 Найдём площадь ограниченной области, лежащей между графиками 
и 
. Эти графики имеют две общих точки 
и 
(см. рис.), причём на отрезке 
график идёт выше, чем график .
Значит, площадь области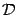 между графиками равна 
и . Эти графики имеют две общих точки и (см. рис.), причём на отрезке график идёт выше, чем график . 
Рис.6.2.
Значит, площадь области
между графиками равна
Пример 6.2 Найдём площадь ограниченной области 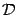, лежащей между графиками 
и 
. Решая уравнение 
, находим, что эти графики пересекаются в трёх точках: 
, и , причём на отрезке 
выше расположен график , а на отрезке -- график . Так как обе функции нечётны, то чертёж обоих графиков симметричен относительно начала координат, и площадь левой части области между графиками (при 
) равна площади правой части области (при 
).
Поэтому искомую площадь можно подсчитать так:
, лежащей между графиками и . Решая уравнение , находим, что эти графики пересекаются в трёх точках: , и , причём на отрезке выше расположен график , а на отрезке -- график . Так как обе функции нечётны, то чертёж обоих графиков симметричен относительно начала координат, и площадь левой части области между графиками (при ) равна площади правой части области (при ). 
Рис.6.3.
Поэтому искомую площадь можно подсчитать так:
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
