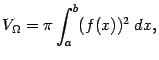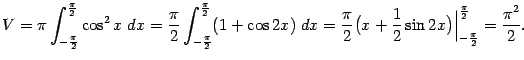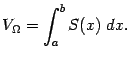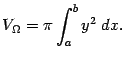‹-- Назад Пусть в пространстве
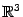
с декартовой системой координат
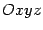
лежит область
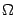
, проектирующаяся на ось

в отрезок
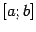
. Предположим, что для каждого
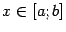
нам известна площадь
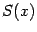
сечения тела
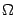
плоскостью, проходящей через точку

оси абсцисс перпендикулярно этой оси. Площадь
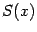
будем называть
площадью поперечного сечения тела
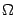
.
Для нахождения объёма тела 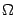 возьмём размеченное разбиение
возьмём размеченное разбиение  отрезка
отрезка 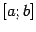 , которое образуют точки деления
, которое образуют точки деления 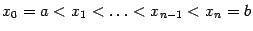 и отмеченные точки
и отмеченные точки 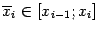 ,
, 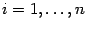 . Плоскости
. Плоскости 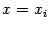 разбивают тело
разбивают тело 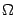 на слои
на слои 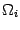 , объёмы которых мы вычислим приближённо, в соответствии с этим разбиением заменив объём слоя
, объёмы которых мы вычислим приближённо, в соответствии с этим разбиением заменив объём слоя 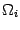 на объём цилиндра, высота которого
на объём цилиндра, высота которого 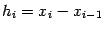 та же, что у слоя
та же, что у слоя 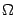 , а основание совпадает с сечением тела плоскостью
, а основание совпадает с сечением тела плоскостью 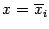 , проведённой где-то посередине между основаниями слоя
, проведённой где-то посередине между основаниями слоя 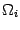 (см. рис.). Образующие этого цилиндра -- отрезки прямых, проходящих параллельно оси
(см. рис.). Образующие этого цилиндра -- отрезки прямых, проходящих параллельно оси  через точки границы сечения.
через точки границы сечения.
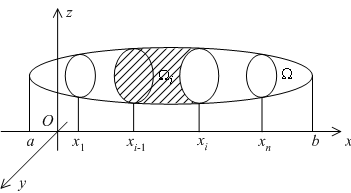
Рис.6.9.
Объём цилиндра равен, очевидно,
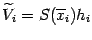
, а подсчитанный приближённо с помощью данного разбиения объём всего тела
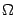
--
Последняя сумма -- это интегральная сумма, построенная для функции
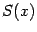
по размеченному разбиению

. При неограниченном измельчении разбиения (то есть при
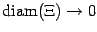
) эта сумма стремится к значению определённого интеграла от
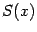
по
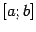
. С другой стороны, задаваемый этой суммой объём будет стремиться к объёму тела
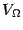
(этот предельный объём мы можем
по определению считать равным
объёму тела 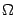
). Итак, получаем формулу
Пример 6.4 Найдём объём ограниченного тела, заключённого между поверхностью цилиндра радиуса
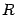
:
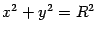
, горизонтальной плоскостью
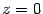
и наклонной плоскостью
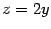
и лежащего выше горизонтальной плоскости
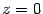
(см. рис.).
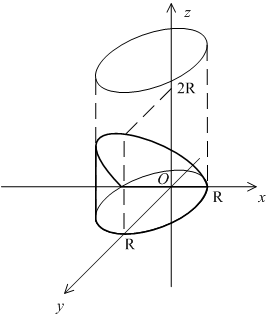
Рис.6.10.
Очевидно, что рассматриваемое тело
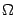
проектируется на ось

в отрезок
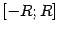
, а при
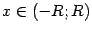
поперечное сечение тела представляет собою прямоугольный треугольник с катетами
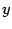
и
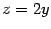
, где
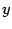
можно выразить через

из уравнения цилиндра:
Поэтому площадь
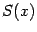
поперечного сечения такова:
Применяя формулу (
6.5), находим объём тела
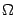
:
Пусть тело 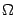 ограничено поверхностью, полученной вращением в пространстве
ограничено поверхностью, полученной вращением в пространстве  линии
линии 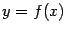 , лежащей в плоскости
, лежащей в плоскости 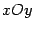 и рассматриваемой при
и рассматриваемой при 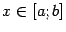 , вокруг оси
, вокруг оси  , а также (с боков) плоскостями
, а также (с боков) плоскостями 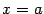 и
и 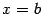 (см. рис.).
(см. рис.).
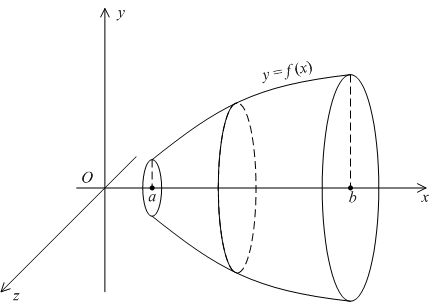
Рис.6.11.
Поскольку поперечными сечениями такого тела вращения служат круги
12 радиуса
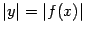
, площадь поперечного сечения будет в этом случае выражаться формулой
а объём тела вращения, как следствие формулы (
6.5), равен
или, более кратко,
Пример 6.5 Пусть в плоскости
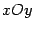
рассматривается линия
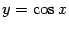
на отрезке
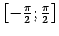
.
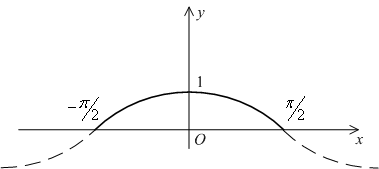
Рис.6.12.
Эта линия вращается в пространстве вокруг оси

, и полученная поверхность вращения ограничивает некоторое тело вращения (см. рис.). Найдём объём
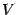
этого тела вращения.
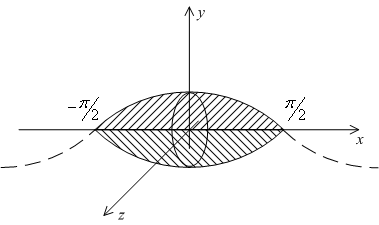
Рис.6.13.
Согласно формуле (
6.6), получаем:
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
![]() возьмём размеченное разбиение
возьмём размеченное разбиение ![]() отрезка
отрезка ![]() , которое образуют точки деления
, которое образуют точки деления ![]() и отмеченные точки
и отмеченные точки ![]() ,
, ![]() . Плоскости
. Плоскости ![]() разбивают тело
разбивают тело ![]() на слои
на слои ![]() , объёмы которых мы вычислим приближённо, в соответствии с этим разбиением заменив объём слоя
, объёмы которых мы вычислим приближённо, в соответствии с этим разбиением заменив объём слоя ![]() на объём цилиндра, высота которого
на объём цилиндра, высота которого ![]() та же, что у слоя
та же, что у слоя ![]() , а основание совпадает с сечением тела плоскостью
, а основание совпадает с сечением тела плоскостью ![]() , проведённой где-то посередине между основаниями слоя
, проведённой где-то посередине между основаниями слоя ![]() (см. рис.). Образующие этого цилиндра -- отрезки прямых, проходящих параллельно оси
(см. рис.). Образующие этого цилиндра -- отрезки прямых, проходящих параллельно оси ![]() через точки границы сечения.
через точки границы сечения. 
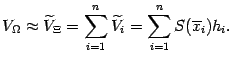

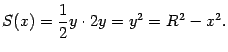
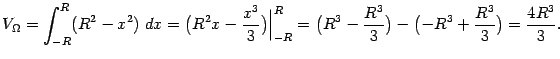
![]() ограничено поверхностью, полученной вращением в пространстве
ограничено поверхностью, полученной вращением в пространстве ![]() линии
линии ![]() , лежащей в плоскости
, лежащей в плоскости ![]() и рассматриваемой при
и рассматриваемой при ![]() , вокруг оси
, вокруг оси ![]() , а также (с боков) плоскостями
, а также (с боков) плоскостями ![]() и
и ![]() (см. рис.).
(см. рис.).