‹-- Назад

Вычисление длины плоской линии

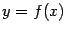
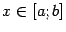
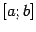
Пусть линия представляет собой график функции , рассматриваемый при . Будем предполагать, что функция имеет на непрерывную производную. Наша цель -- найти длину линии (по сути дела, нам придётся дать определение того, что мы считаем длиной произвольной линии).

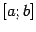Рассмотрим разбиение отрезка точками и отметим соответствующие точки на графике. На каждом отрезке разбиения 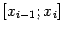приближённо заменим дугу графика 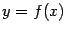на хорду .

Рис.6.14.



Длина этой хорды по теореме Пифагора равняется

Рис.6.15.



Преобразуем это выражение к виду

По теореме Лагранжа, на интервале найдётся такая точка , что

Поэтому получаем

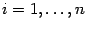
Рассмотрим теперь точки , , как отмеченные точки и получим размеченное разбиение . Соответствующая этому разбиению суммарная длина ломаной равна

Будем считать эту длину приближённым значением длины линии , а предел этой величины при неограниченном измельчении разбиения -- по определению равным длине линии :

Заметим теперь, что величина представляет собой интегральную сумму, составленную по размеченному разбиению для функции . Эта интегральная сумма при измельчении разбиения будет стремиться к значению определённого интеграла, так что получаем в итоге:

(6.7)

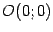
        Пример 6.6   Найдём длину отрезка параболы , лежащего между точками и .

Рис.6.16.



Пусть ; тогда и

Для вычисления значения интеграла проинтегрируем по частям и преобразуем интеграл в правой части так, что получится уравнение относительно :

(6.7*)
(6.8)

Здесь мы учли при перобразовании, что

Последний интеграл в правой части (6.7*) -- табличный:

Получаем в итоге уравнение для искомой величины :

откуда находим

    

Аналогично построению, проведённому выше, можно выполнить построение вписанной ломаной для линии , заданной параметрическими уравнениями в 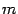-мерном пространстве с координатами :

( для плоскости, для трёхмерного пространства). Снова считая длину линии по определению равной пределу длин вписанных ломаных при измельчении разбиения, получаем формулу для длины дуги линии , лежащей между точками и :

(6.9)

Если на плоскости (то есть при ) в качестве параметра линии, заданной уравнением в полярных координатах , взять полярный угол 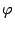, то формула длины линии принимает вид

При выводе этой формулы нужно учесть связь между декартовыми координатами и полярными координатами :

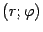
Выведите эту формулу длины из формулы (6.9) в качестве упражнения.

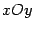
        Пример 6.7   Найдём длину дуги кривой (циклоиды), заданной на плоскости параметрическими уравнениями

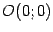
лежащей между точками (соответствует ) и (соответствует ).

Рис.6.17.



Для функций и вычислим производные:

Тогда искомая длина дуги равна

    

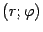
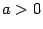
        Пример 6.8   Пусть линия на плоскости с полярными координатами задана уравнением ( ). Поскольку функция периодична с периодом , достаточно рассматривать только значения аргумента , при которых выражение неотрицательно. Кривая имеет вид, изображённый на следующем рисунке.

Рис.6.18.



Найдём длину этой линии.

Имеем

Поэтому искомая длина равна

   
   

    





Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции

на главную
Hosted by uCoz