‹-- Назад
Транспонирование матрицы
Над матрицами определена еще одна операция, называемая транспонированием.
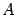
-- матрица размеров 
. Тогда транспонированной матрицей 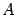называется такая матрица 
размеров 
, что 
, 
, 
. Транспонированная матрица 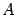обозначается 
или 
. Операция транспонирования заключается в том, что строки и столбцы в исходной матрице меняются ролями. В транспонированной матрице первым столбцом служит первая строка исходной матрицы, вторым столбцом -- вторая строка исходной матрицы и т.д. Например,
Читатель легко проверит, что
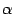
-- число. Доказательство. Пусть
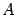
-- матрица размеров , -- матрица размеров 
. Тогда имеет размеры , 
-- размеры 
. Число столбцов в совпадает с числом строк в , поэтому произведение на определено. Размеры этого произведения 
. Матрица 
имеет размеры 
, поэтому 
-- матрица размеров . Итак, матрицы в правой и левой части равенства (14.8) существуют и имеют одинаковые размеры. Пусть 
, 
, 
, 
, 
. Нам нужно показать, что 
, 
, .
По определению транспонирования 
. По определению умножения матриц
С другой стороны,
. 