mathserfer.narod.ru

Теория по высшей математике

‹-- Назад

Производные высших порядков

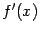
Если функция дифференцируема при всех , то мы можем рассмотреть функцию , сопоставляющую каждой точке значение производной . Эта функция называется производной функции , или первой производной от . (Иногда саму исходную функцию называют нулевой производной и обозначают тогда .) Функция , в свою очередь, может иметь производную во всех (или некоторых) точках интервала , которую мы обозначим и назовём второй производной функции . Если предположить, что вторая производная существует во всех точках , то она может также иметь производную , называемую третьей производной функции , и т. д. Вообще, -й производной функции называется производная от предыдущей, -й производной :

если эта производная существует. -я производная называется также производной -го порядка, а её номер называется порядком производной.

При первую, вторую и третью производные принято обозначать штрихами: или ; при прочих  -- числом в скобках в верхнем индексе: или .

Физический смысл производной второго порядка проясняется из того, что если первая производная 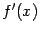задаёт мгновенную скорость изменения значений в момент времени , то вторая производная, то есть производная от 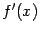, задаёт мгновенную скорость изменения значений мгновенной скорости, то есть ускорение значений . Следовательно, третья производная -- это скорость изменения ускорения (или, что то же самое, ускорение изменения скорости, поскольку, как очевидно следует из определения, ).

Геометрический смысл второй производной связан с понятиями выпуклости и кривизны графика функции, и мы обсудим его ниже.