‹-- Назад
Пусть 
, c -- вектор, отличный от нуля, 
, 
. Попробуем, сложив векторы 
и 
с какими-то коэффициентами, получить 0. Во-первых, сумма 
равна нулю. Но нулевой набор коэффициентов нам ни о чем не говорит: сумма любых векторов с нулевыми коэффициентами равна нулю! Возьмем коэффициенты 
, 
. Получим 
.
Возьмем коэффициенты 2 и 1: 
.
Возьмем коэффициенты 0 и 4: 
.
Возьмем коэффициенты 
и 2: 
. Ура! Ненулевые коэффициенты нашлись, значит, система векторов линейно зависима.
Теперь возьмем два неколлинеарных вектора и .
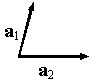
Попробуем составить несколько линейных комбинаций с ненулевыми коэффициентами, чтобы получить нулевой вектор. Возьмем наборы коэффициентов 
, 
, 
, результаты на рисунке.
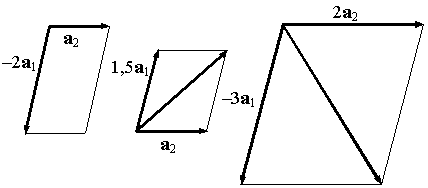
Когда надоест перебирать различные комбинации коэффициентов, заметим, что если оба коэффициента не нулевые, то стороны параллелограмма при построении суммы будут ненулевыми и, следовательно, диагональ длины 0 получиться не может. Если один из коэффициентов равен нулю, а другой отличен от нуля, то линейная комбинация будет равна одному из векторов, умноженному на последний коэффициент, и тоже будет не равна нулю. Таким образом, вектор 
будет равен нулю только при 
. Поэтому система веторов 
является линейно независимой.
Из приведенных примеров можно сделать следующий вывод. Для того, чтобы установить, что система векторов является линейно зависимой, нужно перебирать все возможные наборы коэффициентов, в которых есть хотя бы одно ненулевое число. Как только получится, что линейная комбинация равна нулю, перебор останавливается, и заключаем, что система линейно зависима.
Для того, чтобы установить, что система векторов линейно независимая, нужно перебрать все (бесконечно много!) наборы коэффициентов, в которых есть хотя бы одно ненулевое число, и убедиться, что нулевой вектор никогда не получится. Только в этом случае делаем вывод, что система является линейно независимой.
В действительности линейная зависимость или линейная независимость системы векторов устанавливается другими методами, но об этом позже.
