‹-- Назад Пусть вещественнозначная функция

задана в некоторой области
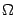
, и

-- некоторое подмножество этой области; тем самым, функция

определена и при всех

. Если теперь рассматривать значения

лишь в точках

, а вне

вообще не рассматривать, то получаем функцию, областью определения которой служит множество

:
Функция

называется
ограничением функции 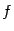 на множество
на множество 
.
Пример 7.8 Функция

определена на всей плоскости

. Рассмотрим в качестве множества

круг

Тогда ограничение

задаётся той же формулой:

, но теперь мы можем брать в качестве аргументов только такие точки

, для которых

, то есть

.
Если же взять за множество  прямую
прямую  с уравнением
с уравнением  на плоскости
на плоскости  , то запись выражения, задающего функцию
, то запись выражения, задающего функцию  , можно будет упростить, использовав уравнение прямой, а именно, либо получить
, можно будет упростить, использовав уравнение прямой, а именно, либо получить
либо
В первом случае задающее ограничение

выражение зависит лишь от

и задаёт функцию одного переменного

:

, где

, а во втором случае -- лишь от
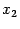
и задаёт другую функцию одного переменного:

, где

.
Функции  и
и  , выражающие значение ограничения через меньшее, по сравнению с исходным, число переменных (в данном примере -- через одну переменную,
, выражающие значение ограничения через меньшее, по сравнению с исходным, число переменных (в данном примере -- через одну переменную,  или
или 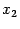 ) называются параметризациями ограничения
) называются параметризациями ограничения  . Те переменные, от которых зависит параметризация, называются параметрами ограничения (точнее, параметрами рассматриваемой параметризации; как показывает приведённый выше пример, одно и то же ограничение
. Те переменные, от которых зависит параметризация, называются параметрами ограничения (точнее, параметрами рассматриваемой параметризации; как показывает приведённый выше пример, одно и то же ограничение  может иметь различные параметризации).
может иметь различные параметризации).
При рассмотрении ограничения функции разумно использовать те параметры, при которых параметризация задаётся более простой формулой.
Пример 7.9 Пусть функция

определена на всей плоскости

с переменными

. Рассмотрим ограничение этой функции на кубическую параболу

, то есть на множество

тех точек плоскости, что связаны уравнением

. Уравнение параболы можно записать также в виде

. Используя эти два уравнения, мы можем получить параметризацию ограничения

с помощью параметра

:
и с помощью параметра
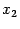
:
По-видимому, вторая параметризация предпочтительнее в силу большей простоты выражения.
Не должно создаваться впечатления, будто параметрами ограничения могут выступать лишь какие-либо из исходных переменных, от которых зависит рассматриваемая функция 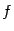 . В следующем примере гораздо более удобной для параметризации служит переменная, равная полярному углу
. В следующем примере гораздо более удобной для параметризации служит переменная, равная полярному углу 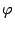 , а не какая-либо из координат
, а не какая-либо из координат  или
или 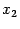 .
.
Пример 7.10 Рассмотрим функцию

, заданную на плоскости

, и окружность

. Ограничение

с параметром
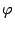
, равным полярному углу, отыскивается тогда с помощью соотношений между декартовыми и полярными координатами:
где
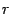
-- полярный радиус, равный

. Тогда уравнение окружности можно записать как

, а функция

будет задаваться равенством
где

.
Заметим, что невозможно получить параметризацию этого ограничения с помощью параметров  или
или 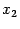 на всей окружности
на всей окружности  сразу: при одном и том же
сразу: при одном и том же  (или
(или 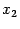 ) в точках окружности, симметричных относительно оси
) в точках окружности, симметричных относительно оси  (или
(или  соответственно), функция
соответственно), функция 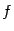 принимает разные значения. Однако если в качестве
принимает разные значения. Однако если в качестве  рассматривать не всю окружность, а, скажем, её верхнюю часть, которая задаётся уравнением
рассматривать не всю окружность, а, скажем, её верхнюю часть, которая задаётся уравнением  , то ограничение на
, то ограничение на  можно будет параметризовать с помощью параметра
можно будет параметризовать с помощью параметра  :
:
где

.
Аналогично можно параметризовать ограничение 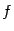 на нижнюю часть окружности, использовав уравнение этой нижней части:
на нижнюю часть окружности, использовав уравнение этой нижней части:  . С помощью параметра
. С помощью параметра 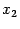 можно параметризовать ограничение
можно параметризовать ограничение 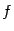 на правую (при
на правую (при  ) или левую (при
) или левую (при  ) половины окружности.
) половины окружности.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
![]() прямую
прямую ![]() с уравнением
с уравнением ![]() на плоскости
на плоскости ![]() , то запись выражения, задающего функцию
, то запись выражения, задающего функцию ![]() , можно будет упростить, использовав уравнение прямой, а именно, либо получить
, можно будет упростить, использовав уравнение прямой, а именно, либо получить 
![]() и
и ![]() , выражающие значение ограничения через меньшее, по сравнению с исходным, число переменных (в данном примере -- через одну переменную,
, выражающие значение ограничения через меньшее, по сравнению с исходным, число переменных (в данном примере -- через одну переменную, ![]() или
или ![]() ) называются параметризациями ограничения
) называются параметризациями ограничения ![]() . Те переменные, от которых зависит параметризация, называются параметрами ограничения (точнее, параметрами рассматриваемой параметризации; как показывает приведённый выше пример, одно и то же ограничение
. Те переменные, от которых зависит параметризация, называются параметрами ограничения (точнее, параметрами рассматриваемой параметризации; как показывает приведённый выше пример, одно и то же ограничение ![]() может иметь различные параметризации).
может иметь различные параметризации). ![]() . В следующем примере гораздо более удобной для параметризации служит переменная, равная полярному углу
. В следующем примере гораздо более удобной для параметризации служит переменная, равная полярному углу ![]() , а не какая-либо из координат
, а не какая-либо из координат ![]() или
или ![]() .
. ![]() или
или ![]() на всей окружности
на всей окружности ![]() сразу: при одном и том же
сразу: при одном и том же ![]() (или
(или ![]() ) в точках окружности, симметричных относительно оси
) в точках окружности, симметричных относительно оси ![]() (или
(или ![]() соответственно), функция
соответственно), функция ![]() принимает разные значения. Однако если в качестве
принимает разные значения. Однако если в качестве ![]() рассматривать не всю окружность, а, скажем, её верхнюю часть, которая задаётся уравнением
рассматривать не всю окружность, а, скажем, её верхнюю часть, которая задаётся уравнением ![]() , то ограничение на
, то ограничение на ![]() можно будет параметризовать с помощью параметра
можно будет параметризовать с помощью параметра ![]() :
: 
![]() на нижнюю часть окружности, использовав уравнение этой нижней части:
на нижнюю часть окружности, использовав уравнение этой нижней части: ![]() . С помощью параметра
. С помощью параметра ![]() можно параметризовать ограничение
можно параметризовать ограничение ![]() на правую (при
на правую (при ![]() ) или левую (при
) или левую (при ![]() ) половины окружности.
) половины окружности.