‹-- Назад Пусть

-- некоторая база, и

и
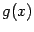
-- функции, заданные на некотором окончании этой базы. В главе 2 мы изучали сравнение функций

и
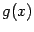
при базе

в случае, когда они является бесконечно малыми. Здесь же мы изучим сравнение бесконечно больших

и
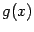
.
Определение 5.1 Пусть

-- бесконечно большие величины при базе

. Они
имеют один и тот же порядок роста при базе

, если существует предел
То, что

и
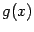
имеют один и тот же порядок роста, обозначим так:
Если при этом

, то бесконечно большие

и
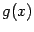
называются
эквивалентными при базе

; это обозначается так:
Если
то величина
 имеет меньший порядок роста
имеет меньший порядок роста при базе

, чем величина
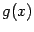
. Этот факт записывается так:
Наконец, если при некотором

имеет место соотношение
то будем говорить, что величина

имеет
порядок роста, равный 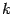
, относительно величины
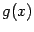
.
Пример 5.7 При

величины

,

,

,

,

,

-- бесконечно большие. При этом

,

,

,

,

,

имеет порядок

относительно

,

имеет порядок 3 относительно

и порядок 6 относительно

,

имеет порядок 4 относительно

и порядок

относительно

.
В качестве простого упражнения докажите упомянутые соотношения; легко увидеть между функциями  ,
,  также много других соотношений.
также много других соотношений.
Пример 5.8 При

рассмотрим функции

(

) и

(

). Покажем, что при всех таких

и

имеет место соотношение
то есть любая степень

имеет меньший порядок роста при

, чем растущая экспонента

.
Для этого рассмотрим предел  . К этому пределу можно применить правило Лопиталя:
. К этому пределу можно применить правило Лопиталя:
Если при этом

, то последний предел берётся от бесконечно малой и равен 0; если же

, то правило Лопиталя можно применить ещё раз и, быть может, неоднократно. В конечном счёте получим
где

(напомним, что через

обозначается ближайшее целое число, не меньшее

). Поскольку

, в числителе дроби стоит невозрастающая функция, а знаменатель стремится к

, так что предел равен 0, что и требовалось получить.
Упражнение 5.1 Докажите, что функция

имеет при

больший порядок роста, чем

, при любом

, и, тем более, чем любой многочлен

Пример 5.9 При

рассмотрим функции

(

) и

(

). Покажем, что при всех таких

и

имеет место соотношение
то есть логарифм имеет меньший порядок роста при

, чем любая положительная степень

.
Для доказательства вычислим предел  Поскольку это предел отношения двух бесконечно больших, можно применить правило Лопиталя:
Поскольку это предел отношения двух бесконечно больших, можно применить правило Лопиталя:
Упражнение 5.2 Докажите, что

при любом, как угодно малом

имеет больший порядок роста при

, чем любая, сколь угодно большая степень логарифма

, (

,

).
Упражнение 5.3 Докажите, что при

степенные функции

,

, имеют тем больший порядок роста, чем больше значение

.
Упражнение 5.4 Докажите, что

при любом, как угодно малом

имеет больший порядок роста при

, чем любая, сколь угодно большая степень логарифма

, (

,

).
Упражнение 5.5 Выясните, какая из функций имеет больший порядок роста при

:
а)

или

?
б)

или

?
Пример 5.10 Рассмотрим функцию

Эта функция непрерывна справа в точке

. Найдём её производную справа в точке 0, сделав при этом замену

:
поскольку, как мы выяснили выше, экспонента

растёт быстрее

при

.
Во всех остальных точках 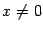 производная вычисляется с помощью правил дифференцирования:
производная вычисляется с помощью правил дифференцирования:
При

это выражение имеет предел
поскольку степень в числителе дроби имеет меньший порядок роста, чем экспонента в знаменателе.
Таким образом, получили, что  , то есть производная оказалась непрерывной справа в точке
, то есть производная оказалась непрерывной справа в точке  .
.
Из того, что функция  -- нечётная, нетрудно найти, чему будет равна производная слева в точке 0 у функции
-- нечётная, нетрудно найти, чему будет равна производная слева в точке 0 у функции  , если её переопределить в нуле так, чтобы она оказалась непрерывной слева. У этой функции производная слева также будет существовать во всех точках
, если её переопределить в нуле так, чтобы она оказалась непрерывной слева. У этой функции производная слева также будет существовать во всех точках  , причём эта левая производная будет всюду непрерывна слева.
, причём эта левая производная будет всюду непрерывна слева.
Пример 5.11 Рассмотрим функцию
При
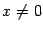
её производная равна, как нетрудно подсчитать,
При

мы найдём производную, исходя из определения:
(мы применили формулу

, а затем сделали замену

). Легко видеть, что предел производной также будет равен 0:
так как

при

растёт быстрее любой степени. Таким образом,
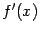
-- функция, непрерывная на всей числовой оси:
Аналогично можно убедиться, что
непрерывная на

функция, и вообще, при любом номере

производная

имеет вид
где

-- некоторый многочлен переменного

. Легко видеть, что эта функция непрерывна при

.
Таким образом, мы получили важный пример функции, которая всюду имеет производные любого порядка, и при этом в точке 0 все эти производные равны 0, в то время как сама функция отлична от 0 при всех 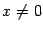 .
.
Упражнение 5.6 Рассмотрите функцию
Покажите, что все её производные существуют при всех

и непрерывны; при этом

для любого

.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции


![]() ,
, ![]() также много других соотношений.
также много других соотношений.  . К этому пределу можно применить правило Лопиталя:
. К этому пределу можно применить правило Лопиталя: 

 Поскольку это предел отношения двух бесконечно больших, можно применить правило Лопиталя:
Поскольку это предел отношения двух бесконечно больших, можно применить правило Лопиталя: 
 Эта функция непрерывна справа в точке
Эта функция непрерывна справа в точке 
![]() производная вычисляется с помощью правил дифференцирования:
производная вычисляется с помощью правил дифференцирования: 

![]() , то есть производная оказалась непрерывной справа в точке
, то есть производная оказалась непрерывной справа в точке ![]() .
. ![]() -- нечётная, нетрудно найти, чему будет равна производная слева в точке 0 у функции
-- нечётная, нетрудно найти, чему будет равна производная слева в точке 0 у функции ![]() , если её переопределить в нуле так, чтобы она оказалась непрерывной слева. У этой функции производная слева также будет существовать во всех точках
, если её переопределить в нуле так, чтобы она оказалась непрерывной слева. У этой функции производная слева также будет существовать во всех точках ![]() , причём эта левая производная будет всюду непрерывна слева.
, причём эта левая производная будет всюду непрерывна слева. 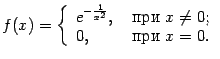


 , а затем сделали замену
, а затем сделали замену 



![]() .
. 