‹-- Назад Используя оценку остаточного члена в форме Лагранжа, можно провести анализ погрешности в формулах приближённого дифференцирования, предполагая шаг 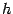 малым.
малым.
Пусть функция  разложена по формуле Тейлора, с остаточным членом в форме Лагранжа, в точке
разложена по формуле Тейлора, с остаточным членом в форме Лагранжа, в точке  . Положим
. Положим 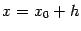 , тогда
, тогда
Отсюда
где

--
погрешность формулы приближённого дифференцирования, получающаяся при замене
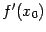
на разностную производную

.
Следовательно,
где
Как правило, заранее известна более грубая оценка для

на некотором отрезке

, включающем в себя

:
и

не зависит от

и
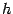
. Тогда
из этой оценки и определяют погрешность вычислений при данном шаге
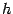
.
Аналогично, можно получить оценку погрешности для разностной производной вида
Ошибку

при замене
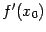
на это отношение можно оценить исходя из разложения

в точке

по формуле Тейлора с остаточным членом в форме Лагранжа порядка 3:
где

. Подставляя сюда

вместо
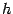
, получаем:
где

. Вычтем из первой формулы вторую:
Отсюда
Если теперь предположить, что
то оценка погрешности получится такая:
Упражнение 6.4 Исследуйте приближённую формулу
Какая степень приращения
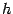
будет множителем в оценке ошибки

? Оценки каких производных войдут в формулу для оценки ошибки?
Подробнее о вопросах численного дифференцирования, в том числе и об оценках возникающих при этом погрешностей, можно прочитать в книгах по методам вычислений, например: [Бахвалов Н. С., Жидков Н. П., Кобельков Г. М., Численные методы. -- М.: Наука, 1987] или [Березин И. С., Жидков Н. П., Методы вычислений. Том 1. -- М.: Наука, 1966].
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
![]() малым.
малым. ![]() разложена по формуле Тейлора, с остаточным членом в форме Лагранжа, в точке
разложена по формуле Тейлора, с остаточным членом в форме Лагранжа, в точке ![]() . Положим
. Положим ![]() , тогда
, тогда 

 --
--  .
. 






