mathserfer.narod.ru

Теория по высшей математике

‹-- Назад

Производные неявно заданной функции

Пусть дана дифференцируемая функция , для которой в некоторой точке выполнено неравенство

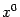
Тогда в некоторой окрестности точки уравнение

определяет, как мы знаем из теоремы о неявной функции, некоторую функцию , заданную вблизи точки в .

Пусть требуется найти её частные производные , . Это можно сделать, применив формулу производной сложной функции к функции

которая тождественно равна 0 в окрестности точки ; следовательно, и все её частные производные в точке обращаются в 0. Итак, считая параметром, от которого зависят все аргументы функции , переменную , где , получаем по формуле :

(производные равны 0 при , ), то есть

откуда

или

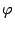
Эта важная формула позволяет вычислять производные неявно заданной функции , не имея задающего её явного выражения.

---