‹-- Назад
Касательная плоскость к графику функции
Пусть дана функция двух переменных
, заданная в некоторой области 
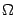
, и точка 
такова, что существуют частные производные 
и 
, непрерывные в точке 
. Рассмотрим график данной функции: 
и его сечения вертикальными плоскостями 
и 
. Как отмечалось выше, прямые, касательные к сечениям графика в этих плоскостях, наклонены, соответственно, к осям 
и 
под углами 
и 
, такими, что 
и 
.
Проведём плоскость через эти две взаимно перпендикулярные касательные. Эта плоскость будет касательной к поверхности графика
. Найдём её уравнение. Запишем уравнение
где
, и покажем, что плоскость (7.13) в пространстве 
, где расположен график, обладает нужными свойствами. Действительно, эта плоскость проходит через точку касания 
, что проверяется подстановкой координат этой точки в уравнение плоскости (7.13). При , то есть в сечении плоскости (7.13) вертикальной плоскостью , получаем
равен
пересекается с плоскостью (7.13) в точности по касательной этого вертикального сечения. Уравнение (7.13) можно записать также в виде
Прямая, проходящая через точку касания перпендикулярно касательной плоскости к поверхности , называется нормалью к этой поверхности, проведённой в точке , или нормальной прямой.
Поскольку вектор
и 
в уравнении касательной плоскости) и, следовательно, параллелен нормали, проведённой через точку касания, то уравнения нормали мы получим как канонические уравнения прямой, проходящей через заданную точку параллельно известному вектору 
:
. (Заметим, что эта поверхность -- график функции 
-- эллиптический параболоид.) 
Частные производные от
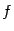
, вычисленные в точке 
, равны
(касательная плоскость)
(нормаль)
Заметим, что касательная плоскость pасположена гоpизонтально, то есть задаётся уpавнением 
, если значения частных пpоизводных в точке 
pавняются 0:
называются стационаpными точками функции .
