mathserfer.narod.ru

Теория по высшей математике

Возрастание и убывание функции

Возрастание и убывание дифференцируемой функции связано со знаком её производной. Напомним, что функция называется возрастающей на интервале , если для любых двух точек из неравенства следует, что ; убывающей на интервале , если из неравенства следует, что ; невозрастающей на интервале , если из неравенства следует, что , и неубывающей на интервале , если из неравенства следует, что .

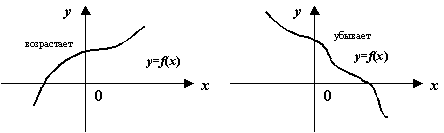
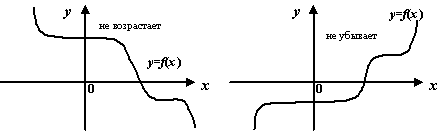
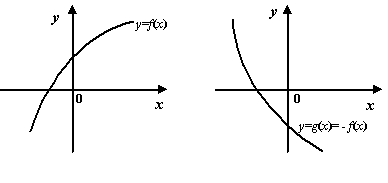
Очевидно, что функция возрастает тогда и только тогда, когда убывает функция ; аналогичное утверждение связывает неубывающую функцию с невозрастающей.

Рис.7.16.Графики функций и

        Теорема 7.2   Пусть функция дифференцируема на интервале и при всех . Тогда возрастает на . Если же при всех , то не убывает на .

Аналогично, если при всех , то убывает на , а если при всех , то не возрастает на .

        Доказательство.     В силу предыдущего замечания, теорему достаточно доказывать только для случаев и . Пусть при всех и , . Применим к отрезку формулу конечных приращений:

Точно так же, если , то получаем , откуда , что означает неубывание функции.     

Имеет место и утверждение, "почти обратное" к предыдущей теореме:

        Теорема 7.3   Если дифференцируемая функция не убывает на интервале , то при всех ; если же функция не возрастает на , то при .

        Доказательство.     Фиксируем точку и рассмотрим предел, который равен производной:

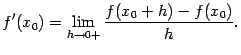
Вторая часть утверждения теоремы доказывается аналогично.     

Заметим, что усилить утверждение теоремы нельзя: из того, что функция возрастает на не следует строгого неравенства для производной. Действительно, в этом нас убеждает простой пример:

        Пример 7.15   Рассмотрим функцию . Эта функция дифференцируема всюду и возрастает на всей оси : из следует, что . Однако неверно, что при всех : действительно, производная обращается в 0 при .     

Итак, всё, что мы можем гарантировать в случае строгого возрастания (как и в случае нестрогого возрастания, то есть неубывания) -- это нестрогое неравенство .

Практический смысл полученных утверждений о связи возрастания и убывания со знаком производной -- в том, что для того, чтобы найти интервалы возрастания функции , надо решить относительно неравенство , а чтобы найти интервалы убывания -- решить неравенство .

        Пример 7.16   Рассмотрим функцию . Её производная такова:

Интервал возрастания функции можно найти из неравенства

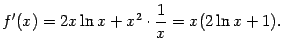
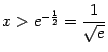При решении этого неравенства учтём, что в области определения функции , так что нужно решать неравенство . Отсюда . Таким образом, функция 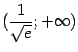возрастает на интервале . Нетрудно видеть, что при 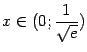выполняется обратное неравенство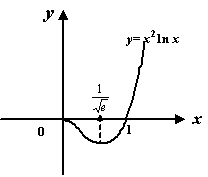 , так что на этом интервале функция убывает.     

Рис.7.17.График функции

Если два интервала возрастания функции примыкают друг к другу, то есть имеют вид и , и функция непрерывна в точке , то эти два смежных интервала можно объединить: функция будет возрастать на . То же, разумеется, относится и к смежным интервалам убывания функции.

        Пример 7.17   Рассмотрим функцию . Её производная имеет вид

Решая неравенство , получаем: ; при функция, очевидно, непрерывна, так что возрастает на объединённом интервале, то есть при . Решение неравенства даёт только один интервал ; на нём функция убывает.     

Рис.7.19.График функции

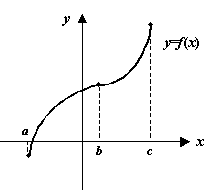
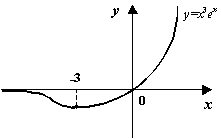
Геометрический смысл связи знака производной с направлением изменения функции легко виден из геометрического смысла производной: если угловой коэффициент касательной к графику (равный производной) положителен, то угол наклона касательной -- острый, что соответствует графику возрастающей функции. Если же угловой коэффициент отрицателен, то угол наклона касательной -- тупой, и тогда функция убывает.