‹-- Назад
Извлечение корня из комплексного числа
Заголовок этого раздела является не совсем точным. Дело в том, что корень из ненулевого комплексного числа однозначно определить нельзя. Он всегда имеет столько значений, какова его степень. Поэтому в данном разделе мы будем говорить о решении уравнения
где неизвестным служит
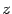
, а 
-- известное комплексное число. Но поскольку в школе решение этого уравнения записывалось в виде 
, то, не слишком соблюдая математическую строгость, можно говорить, что мы будем извлекать корень 
-ой степени из комплексного числа . Итак, решаем уравнение (17.14). Если 
, то 
. Пусть 
. Запишем число в тригонометрической форме: 
. Здесь 
и 
-- известные величины. Запишем неизвестное число 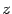в тригонометрической форме: 
. Здесь 
и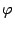 
-- неизвестны. По формуле Муавра
. В этом соотношении и -- положительные числа, следовательно 
, где справа стоит обычный арифметический корень из положительного числа. Если два комплексных числа равны, то аргументы у них могут различаться только на величину, кратную 
. Поэтому 
, 
. Отсюда находим, что
Значения
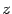
, отличные от указанных в этой формуле, дадут те же значения , которые можно получить при 
. Решение. Запишем число 
в тригонометрической форме:
, 
. Тогда
получим:
получим:
получим:
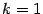
получим:
Ответ: 
, 
, 
, 
.
