‹-- Назад Пусть в области

задана функция

, которая в некоторой точке

имеет частные производные

по всем переменным
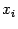
,
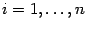
.
Определение 8.1 Вектор, компонентами которого служат значения частных производных, то есть вектор
называется
градиентом функции

, вычисленным в точке
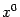
. Градиент
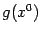
обозначается также

и

.
Если частные производные существуют во всех точках области 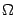 , то градиент, вычисленный в произвольной переменной точке
, то градиент, вычисленный в произвольной переменной точке  , представляет собой вектор-функцию
, представляет собой вектор-функцию  со значениями в
со значениями в 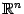 .
.
В некоторых точках 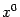 градиент может оказаться нулевым вектором. Тогда значения всех частных производных в точке
градиент может оказаться нулевым вектором. Тогда значения всех частных производных в точке 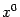 будут равны 0:
будут равны 0:

при всех

Такие точки
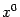
называются
стационарными точками функции

.
Пример 8.1 Рассмотрим функцию

, заданную на всей плоскости

. Поскольку
то
а стационарные точки задаются системой уравнений
Решая эту систему из двух линейных уравнений, находим единственное решение:
Значит,

-- единственная стационарная точка этой функции.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
 по всем переменным
по всем переменным 
![]() , то градиент, вычисленный в произвольной переменной точке
, то градиент, вычисленный в произвольной переменной точке ![]() , представляет собой вектор-функцию
, представляет собой вектор-функцию ![]() со значениями в
со значениями в ![]() .
. ![]() градиент может оказаться нулевым вектором. Тогда значения всех частных производных в точке
градиент может оказаться нулевым вектором. Тогда значения всех частных производных в точке ![]() будут равны 0:
будут равны 0:  при всех
при всех 
