mathserfer.narod.ru

Теория по высшей математике

Определение и примеры

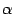
        Определение 18.1   Пусть  -- поле,  -- некоторое множество, на котором задана операция сложения, обозначаемая знаком "+", и операция умножения на элемент поля , то есть любому элементу , , и любому элементу , , сопоставляется элемент из множества , называемый произведением 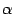на и обозначаемый . Множество называется линейным или векторным пространством над полем , если по отношению к операции сложения множество является абелевой группой, и для любых из поля и любых из множества выполнены равенства:

1. ;
2. ;
3. ;
4. , где 1 -- единица поля .

        

В дальнейшем в качестве поля используется или поле вещественных чисел, или поле комплексных чисел. В первом случае множество называется вещественным линейным пространством, во втором -- комплексным линейным пространством.

Легко проверить, что множество векторов трехмерного простраства является вещественным линейным пространством. Действительно, первые четыре свойства векторов из теоремы 10.1 означают, что векторы образуют абелеву группу по сложению, а последние четыре свойства из той же теоремы соответствуют требованиям 1-4 к операции умножения на элементы поля (в данном случае на вещественные числа).

По аналогии с трехмерным векторным пространством элементы любого линейного пространства называются векторами, хотя природа этих элементов может быть совсем иная.

Другими примерами вещественных линейных пространств могут служить:

1. множество столбцов из элементов, являющихся вещественными числами ;
2. множество многочленов степени не выше с вещественными коэффициентами;
3. множество всех многочленов с вещественными коэффициентами;
4. множество функций непрерывных на некотором отрезке .

Если в примерах 1-3 слово "вещественными" заменить на "комплексными", то получим примеры комплексных линейных пространств.

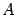
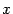
        Пример 18.1   Рассмотрим еще один пример линейного пространства. Пусть имеется однородная система линейных уравнений, которую запишем в матричном виде , где  -- матрица системы, а  -- столбец неизвестных. В силу  предложения 15.3 столбцы-решения системы можно складывать и умножать на число. При этом будут получаться снова решения этой системы. Значит, на множестве решений определены операции сложения и умножения на число. Легко проверить, что эти операции удовлетворяют требованиям из определения линейного пространства. Итак, множество решений однородной системы линейных уравнений является линейным пространством. 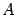Если матрица имеет вещественные элементы, то и пространство будет вещественным, если комплексные -- то и пространство будет комплексным.