‹-- Назад

Производная по направлению

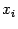
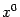
Пусть снова функция задана в области и имеет во всех точках частные производные по всем переменным . Предположим, что все частные производные непрерывны в точке . Тогда функция длифференцируема в точке , то есть приращение функции имеет главную линейную часть, которая равна дифференциалу:

где  -- величина большего порядка малости при , чем . Напомним, что

так что получаем

(8.1)

Фиксируем теперь в какое-нибудь направление, выбрав задающий его ненулевой вектор Через точку 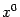в направлении вектора 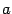проходит некоторая ось . (Напомним, что осью называется прямая с выбранным на ней направлением, то есть выбранным порядком следования точек.) Точки этой оси можно задать параметрическими уравнениями:

или, в векторном виде, , где и увеличению значений параметра соответствует движение точки оси в направлении вектора .

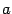
Обозначим ту часть оси , которая состоит из точек оси, следующих после 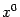, то есть точек луча , получающегося при .

        Определение 8.2   Значение предела

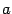
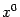
называется производной функции по направлению оси (или луча) (или по направлению вектора ), вычисленной в точке . Производная по направлению обозначается или     

Смысл определения производной по направлению -- в том, что она задаёт мгновенную скорость изменения значений функции при прямолинейном и равномерном движении точки вдоль оси в момент .

Заметим, что если направление оси совпадает с направлением одной из координатных осей , то производная функции 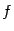по такому направлению, очевидно, равняется (правой) производной функции 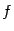по соответствующей переменной 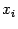. Если существует (двусторонняя) частная производная по 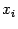, то получаем, что

если .

Используя параметризацию точки на луче вида и замечая, что условие означает, что , получаем:

Запишем теперь приращение функции, стоящее в числителе, через частные производные с помощью формулы (8.1):

   

Отсюда

   
   

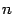
Здесь в правой части первые слагаемых не зависят от . Поскольку при , то последний предел равен 0, так как  -- величина большего порядка малости, чем . Итак, получили формулу

С помощью этой формулы можно вычислять производную по любому направлению, если известен направляющий вектор этого направления .

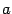
Заметим, что в правой части полученной формулы первый множитель каждого слагаемого -- это компонента вектора , а второй множитель -- компонента вектора . Этот вектор лишь длиной отличается от вектора 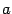; направление его, очевидно, то же, что у 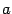. Длина вектора равна 1:

Поэтому компоненты вектора  -- это направляющие косинусы -- косинусы углов между осью и осями координат :

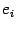
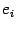
где  -- единичный направляющий вектор оси , , а точкой обозначено скалярное произведение векторов и . Таким образом, имеет место следующая теорема, выражающая связь между производной по направлению, градиентом и единичным направляющим вектором оси:

        Теорема 8.1   Если все частные производные функции непрерывны в точке и направление оси задано вектором , то

где  -- единичный направляющий вектор оси , или

где  -- углы между осью и осями .     





Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции

на главную
Hosted by uCoz