‹-- Назад
Упражнения и задачи
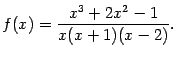
Подсказка:
Рассмотрите точки 
, в которых знаменатель обращается в 0. Внимание: в одной из этих точек вертикальной асимптоты нет, так как функция имеет устранимый разрыв.
Решение:
Область определения составляют все точки оси 
, кроме 0, 
и 2:
числитель также обращается в 0: 
. Деление столбиком даёт: 
дробь 
можно сократить на 
: 
функция стремится к 
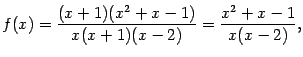
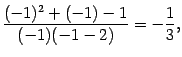а не к 
. При , равном двум другим корням знаменателя, 0 и 2, числитель в 0 не обращается, а равен и 
соответственно. Значит, при 
и при 
, и прямые 
и 
-- вертикальные асимптоты.
Ответ:
и .
а)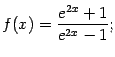 
б)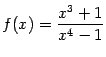 
;
в)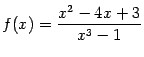 
.
Ответы: а) ; б) 
; в) вертикальных асимптот нет.
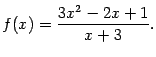
Подсказка:
Воспользуйтесь общими формулами для 
и 
в уравнении асимптоты 
. Пределы при 
и при 
здесь можно искать заодно.
Решение:
Найдём и :
 | |
 |
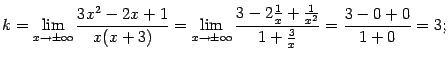
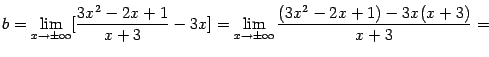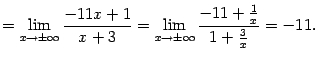Итак, прямая
служит наклонной асимптотой графика 
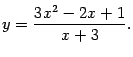
Ответ: наклонная асимптота при 
имеет уравнение .
а)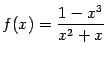 
;
б)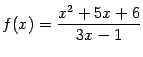 
;
в)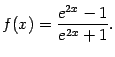 
Ответы: а) 
при ; б) 
при ; в) 
при и 
при .
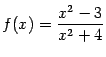на отрезке 
. Подсказка:
Найдите стационарные точки функции, попадающие на заданный отрезок, и добавьте к ним концы отрезка. В одной из этих точек функция будет принимать наибольшее, а в другой -- наименьшее значение.
Решение:
Поскольку знаменатель дроби положителен при всех , функция непрерывна на всей оси . Поэтому все её критические точки -- стационарные. Найдём производную:
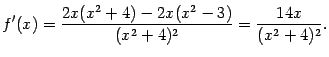
; эта стационарная точка лежит на заданном отрезке . Вычисляем значения функции в этой стационарной точке и в концах отрезка:
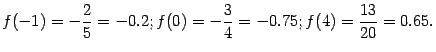
Ответ:
а) 
на отрезке 
;
б)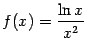 
на отрезке 
;
в) 
на отрезке 
.
Ответы: а) 
;
б)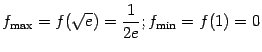 
;
в) 
.
. Подсказка:
Найдите производную и решите неравенства 
и 
.
Решение:
Производная равна 
. Неравенство 
имеет решение 
; на этих двух интервалах возрастает. Неравенство 
имеет решение 
; на этом интервале убывает. Следовательно, точка -- точка локального максимума, а точка 
-- точка локального минимума.
Ответ:
Интервалы возрастания: 
и 
; интервал убывания: 
; точка локального максимума: , точка локального минимума: .
а) 
;
б)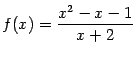 
;
в) 
.
Ответы: а) интервалы возрастания: 
и 
; интервалы убывания: 
и 
; точка локального максимума ; точки локального минимума 
;
б) интервалы возрастания: 
и 
; интервалы убывания: 
и 
; точка локального максимума 
; точка локального минимума 
;
в) интервал возрастания: 
; интервалы убывания: 
и 
; точка локального минимума ; точек локального максимума нет.
Подсказка:
Стационарные точки задаются уравнением 
. Если вторая производная в стационарной точке положительна, то это точка локального минимума, а если отрицательна, то точка локального максимума.
Решение:
Найдём производную: 
; стационарные точки задаются уравнением 
, то есть это точки и 
. Вторая производная равна 
. Её значение в стационарных точках: 
; 
. Следовательно, в точке -- локальный максимум, а в точках и -- локальный минимум.
Ответ:
Имеется три стационарные точки: , 0 и 1; и 1 -- точки локального минимума, а 0 -- точка локального максимума.
а) 
;
б)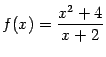 
;
в) 
.
Ответы: а) 
-- точка локального максимума; 
-- точка локального минимума;
б) 
-- точка локального максимума; 
-- точка локального минимума;
в) 
-- точка локального минимума; точек локального максимума нет.
Подсказка:
Интервалы выпуклости задаются неравенством 
, а интервалы вогнутости -- неравенством 
.
Решение:
Найдём вторую производную:
имеет решение 
; на этом интервале функция выпукла. Неравенство 
имеет решение 
; на этих двух интервалах функция вогнута. В точках 
и 
функция меняет направление выпуклости, так что эти точки являются точками перегиба.
Ответ:
Интервал выпуклости: 
; интервалы вогнутости: 
и 
; точки перегиба: 
и 
.
а) 
;
б) 
;
в)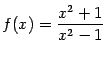 
.
Ответы: а) Интервалы выпуклости: 
и 
; интервал вогнутости: 
; точки перегиба: 
и 
.
б) Интервалы выпуклости: 
и 
; интервал вогнутости: 
; точки перегиба: 
и .
в) Интервалы выпуклости: 
и ; интервал вогнутости: 
; точек перегиба нет.
а)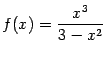 
;
б) 
;
в) 
.
Ответы: а) Функция нечётная;
и 
, наклонная асимптота 
. Точка локального максимума 
, при этом 
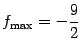; точка локального минимума 
, при этом 
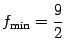. Единственная точка перегиба .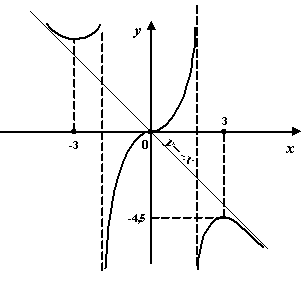 
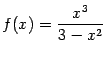
б) Функция чётная; 
; горизонтальная асимптота 
. Точки локального максимума ; значение в этих точках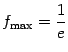 
; точка локального минимума . Четыре точки перегиба: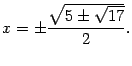 
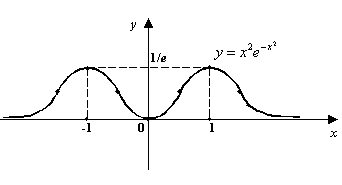
в) Функция нечётная; ; асимптоты 
при и 
при . Точка локального максимума , при этом 
; точка локального минимума , при этом 
. Единственная точка перегиба .
